Clasificación por Bordes en Caribbean Stud

El juego de mesa Caribbean Stud (CS) solía ser uno de los juegos de mesa propietarios más populares del país. En 1994, había 167 mesas de CS en Nevada. En el año 2000, la cifra descendió a 97 mesas. En 2009, solo quedaban 15 mesas. Según los últimos datos de la Nevada Gaming Control Board, en noviembre de 2012, ya no quedaban mesas. Sin embargo, el juego sigue siendo muy popular a nivel internacional. Por ejemplo, hay cientos de mesas de CS en Macao. 

En el CS, los jugadores no pueden compartir sus manos entre sí. El experto jugador con ventaja, James Grosjean, aborda detalladamente la colusión de jugadores en el CS en su libro “Beyond Counting” (Más allá del conteo), en el que describe el conteo “MAK” (MAK = “matches” [coincidencias], “aces” [ases], “kings” [reyes]). Grosjean afirma lo siguiente: “En una mesa completa de siete jugadores, la ventaja sería casi del 2 % si se emplea la estrategia de las 36 cartas, en caso de que los jugadores vean la carta quemada”. 

Grosjean también considera la situación en la que el jugador con ventaja conoce una o más hole cards (cartas de mano), además de la carta bocarriba del crupier. Grosjean aporta los siguientes datos sobre la ventaja de la hole card (carta de mano): 

• Si el jugador con ventaja conoce una carta (la carta bocarriba del crupier), la ventaja de la casa es del 5,23 %.
• Si el jugador con ventaja conoce dos cartas (incluida la carta bocarriba del crupier), la ventaja de la casa es del 1,74 %.
• Si el jugador con ventaja conoce tres cartas (incluida la carta bocarriba del crupier), la ventaja del jugador es del 11,57 %.
• Si el jugador con ventaja conoce cuatro cartas (incluida la carta bocarriba del crupier), la ventaja del jugador es del 35,21 %.
• Si el jugador con ventaja conoce las cinco cartas del crupier, la ventaja del jugador es del 64,27 %. 

No voy a repetir aquí las estrategias para las hole cards (cartas de mano) de Grosjean porque no he copiado su trabajo. El CS fue probablemente una excelente oportunidad a finales de los noventa, ya que era uno de los pocos juegos propietarios ofertados: los casinos todavía no entendían los peligros de la colusión y la exposición de las hole cards (cartas de mano). Pero eso era antes...

Hace poco me contaron una situación en la que un equipo fue descubierto utilizando la clasificación por bordes para ganar al CS. Según mis fuentes, el equipo clasificó los ases y los reyes en una dirección y el resto de cartas en la dirección contraria. Después de ser descubiertos y expulsados, quedaba una pregunta sin responder: ¿cómo de fuerte era su ventaja? 

Antes de abordar esta cuestión, es oportuno incluir un breve resumen. El CS se juega con una sola baraja de cartas. El juego es similar al Three Card Poker, con la estructura común del ante/subir/calificar. Estas son las reglas del CS: 

1. El jugador realiza una apuesta “ante”.
2. El jugador y el crupier reciben cinco cartas cada uno. Cuatro de las cartas del crupier se reparten bocabajo y una de las cartas del crupier se reparte bocarriba.
3. Tras inspeccionar sus cartas y la carta bocarriba del crupier, el jugador puede retirarse y perder su apuesta ante, o puede “subir” la apuesta para permanecer en la mano. La apuesta que se sube equivale a dos veces la apuesta ante.
4. A continuación, el crupier muestra sus cartas. La mano del crupier debe incluir un as/rey o superior para calificar.
5. Si el crupier no califica, el jugador gana el doble de su apuesta ante y la apuesta que se sube es un empate.
6. Si el crupier califica, el jugador compite contra el crupier.
7. Si el crupier califica y vence al jugador, el jugador pierde su apuesta ante y la apuesta que se sube.
8. Si el crupier califica y empate con el jugador, la apuesta ante y la apuesta que se sube quedan en empate.
9. Si el crupier califica y el jugador gana al crupier, el jugador gana el doble de su apuesta ante y recibe la apuesta que se sube según la tabla de pagos de bonus. 

Esta es la tabla de pagos de bono más común para las apuestas que se suben: 

1. La escalera real paga 100 a 1.
2. La escalera de color paga 50 a 1.
3. El poker paga 20 a 1.
4. El full paga 7 a 1.
5. El color paga 5 a 1.
6. La escalera paga 4 a 1.
7. El trío paga 3 a 1.
8. La doble pareja paga 2 a 1.
9. Todo lo demás paga 1 a 1. 

Una estrategia de jugador óptima, pero muy compleja, genera una ventaja de la casa del 5,224 %. El jugador no renuncia a tanto si utiliza una estrategia más sencilla como la de subir con AKJ83 (de palos diferentes) o superior. En este caso, la ventaja de la casa es del 5,316 %. Aquí puedes consultar el análisis matemático completo para el CS. 

A continuación, consideraremos a un jugador con ventaja que ponga en práctica la clasificación por bordes en el CS. Existen muchas formas de clasificar las cartas, pero la clasificación de los ases/reyes parece obvia. Supongamos que el jugador con ventaja clasifica las cartas en estos dos grupos: 

• Cartas altas = {K, A}
• Cartas bajas = {2, 3, 4, 5, 6, 7, 8, 9, T, J, Q}. 

Supongamos que toda la baraja está perfectamente clasificada, de manera que los ases y los reyes estén clasificados en una dirección y el resto de cartas en la dirección contraria. Debido a la forma en que se reparte el CS, es probable que el jugador con ventaja pueda ver las cinco cartas y, por tanto, obtener información sobre si la carta bocabajo del crupier es alta o baja, además de saber la carta bocarriba específica. He decidido utilizar la información de clasificación en su forma más básica. A saber, el jugador con ventaja simplemente sabrá cuántas de las cartas del crupier son altas y cuántas son bajas. 

El jugador con ventaja observa su mano. A continuación, mira la mesa y cuenta el número de cartas altas, que será uno de los siguientes números: 0, 1, 2, 3, 4 o 5. Este total incluye la carta bocarriba del crupier, que también puede ser un as/rey. Con base a la mano del jugador con ventaja y el número de cartas altas del crupier, el jugador con ventaja decide subir o retirarse. Mi siguiente paso fue encontrar los puntos clave de la estrategia de subir/retirarse para cada número de las cartas altas, 0, 1, 2, 3, 4 o 5. Esto lo hice mediante un programa combinatorio que lentamente ofrecía una respuesta para cada una de las cartas altas del crupier. Me sentí como un cerebrito matemático disfrutando mientras el programa encontraba las respuestas. 

Esta es la estrategia óptima para subir/retirarse con base al número de cartas altas en la mano del crupier. 

• Si el crupier no tiene ninguna carta alta, sube con cualquier mano que sea 3/3/4/5/6 o mejor.
• Si el crupier tiene una carta alta, sube siempre.
• Si el crupier tiene dos cartas altas, sube con cualquier mano que sea A/K/J/T/7 o mejor.
• Si el crupier tiene tres cartas altas, sube con cualquier mano que sea A/A/2/3/4 o mejor.
• Si el crupier tiene cuatro cartas altas, sube con cualquier mano que sea A/A/K/K/5 o mejor.
• Si el crupier tiene cinco cartas altas, sube con cualquier mano que sea 2/2/2/2/3 o mejor. 

Por ejemplo, si el jugador con ventaja sabe que tres de las cuatro cartas bocabajo del crupier son cartas altas y la carta bocarriba del crupier es un dos, el crupier tiene un total de tres cartas altas. Según la estrategia anterior, el jugador con ventaja juega con A/A/2/3/4 o superior. Compara esta situación con la que se produce cuando el jugador con ventaja sabe que dos de las cuatro cartas bocabajo del crupier son cartas altas y la carta bocarriba es un as. De nuevo, el jugador con ventaja debería jugar con A/A/2/3/4 o superior. Estas situaciones son muy diferentes, pero la estrategia anterior las trata del mismo modo. Sin duda, se podría mejorar la estrategia si se añadiera el valor específico de la carta bocarriba del crupier. 

En una simulación en la que se jugaran un billón de rondas (1.000.000.000) de CS, esta estrategia daría al jugador una ventaja del 6,90 %. El jugador con ventaja que practica la clasificación por bordes sube el 68,83 % de sus manos y retira el 31,17 % de las manos. En comparación, un jugador sin ventaja que utilice una estrategia de CS óptima, sube el 52,23 % de sus manos. 

Este es un desglose de combinaciones de los posibles resultados para el jugador que emplee la clasificación por bordes CS, según mi simulación:

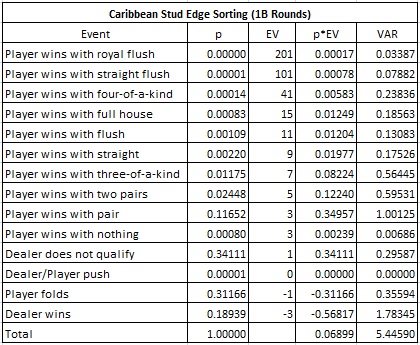
La protección del juego en la clasificación por bordes depende de una decisión táctica y una decisión estratégica. 

• Decisión táctica: asegúrate de que se incluya un giro cada vez que se baraje, incluso cuando el juego se reparta mediante un barajador automático.
• Decisión estratégica: utiliza cartas seguras.