En varios posts anteriores examiné el juego con ventaja con respecto a las devoluciones de pérdidas. Estos incluían dos publicaciones sobre Don Johnson, otros sobre la devolución de pérdidas en el Bacará y estas dos publicaciones sobre la devolución de pérdidas en la ruleta. Mi metodología ha consistido en realizar varias simulaciones de diversos puntos de retirada con ganancias y con pérdidas para encontrar aquellos que maximicen el retorno del jugador. Mediante la simulación del juego real, estos resultados aportan cifras muy precisas dentro de las limitaciones del tamaño de la simulación. Con este cálculo numérico de fuerza bruta, una parte de mí sabía que había una forma más sencilla de resolver esto mediante un enfoque teórico.
Retrocedamos a mi tercer año de universidad (1981). En el semestre de primavera de ese año, asistí como oyente a un curso llamado “Procesos estocásticos”. Con asistir me refiero a que me senté en la clase, pero no tomé apuntes, ni hice los deberes, ni tenía un libro de texto, ni hice ningún examen. Yo estudiaba la carrera de “Teoría de números algebraicos” y este contenido quedaba muy lejos de mis estudios principales. Sé desde hace un tiempo que este tema se aplica directamente a las devoluciones de pérdidas, pero sin libros ni apuntes que mirar, he optado por el método abreviado e infalible del cálculo numérico. Con la reciente publicidad que ha recibido la utilización de devoluciones de pérdidas de Don Johnson, me dispongo a recuperar esos viejos teoremas y a averiguar cómo ponerlos en práctica. Fue muy fácil encontrar información esencial gracias a una búsqueda en Google.
En el libro An Introduction to Stochastic Modeling, de Howard M. Taylor y Samuel Karlin, 3.a edición, 1998 por Academic Press, encontré estos dos teoremas (haz clic en las imágenes para ampliarlos y que sean más fáciles de leer):
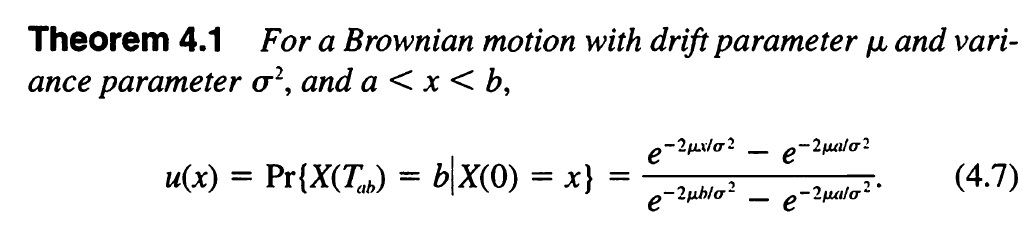
Está claro que parece complicado. Pero resulta que son idóneos para nuestro objetivo. Unos cinco minutos me bastaron para escribir el siguiente teorema que reformulaba estos resultados en términos que permitieran su aplicación a la devolución de pérdidas:

No sabía cómo convertir esas fórmulas en una publicación de blog, de ahí que las imágenes de arriba se lean con dificultad. Haz clic en la imagen de arriba para verla a tamaño completo.
El lector puede preguntarse el motivo por el cual se usa el símbolo de “aproximadamente igual a” en lugar del de igualdad. El motivo es que en los Teoremas 4.1 y 4.2, se supuso que la distribución subyacente era normal mientras que en los juegos de casino las distribuciones discretas no son normales. Un teorema correcto de devolución de pérdidas cuantificaría el carácter concreto de “aproximadamente igual a”. Perdóname por no profundizar más en este tema.
Las distribuciones que no son normales presentan algunas limitaciones prácticas en la precisión de estas fórmulas para simular los juegos de casinos. Por ejemplo, funcionan mucho mejor en el Bacará y el Blackjack que en Video Poker y las tragaperras online. Estas fórmulas también funcionan mejor cuando b es mucho mayor que x, de modo que no funcionan bien con objetivos de ganancia modestos cuando el saldo del jugador importante.
Mi objetivo en este intento teorético es ser capaz de determinar con rapidez los valores de b y x que maximizan los retornos de los jugadores con ventaja en un juego (G) y con una devolución de pérdidas (L). Con este fin, primero programé un programa informático para generar los valores obtenidos de las tres fórmulas del teorema de la devolución de pérdidas para cualquier valor de b y x. Para cualquier situación, modifiqué el programa con una lógica adicional que pudiera resolver el problema de maximizar las ganancias para el jugador con ventaja; es decir, encontrar la mejor b y x posibles. Entonces, mi programa produjo el punto de retirada por pérdidas del jugador, su punto de retirada por ganancias, su probabilidad de ganar, su tiempo de juego esperado y su cantidad de ganancias. La programación me llevo sobre una hora y completar cada cálculo, cuestión de milisegundos.
Algunas veces me gustaría darme un puntapié a mí mismo por ser tan vago intelectualmente.
Ejemplo 1. Don Johnson, Blackjack.
En este ejemplo utilizo el asalto de Don Johnson en Atlantic City. El juego en el que participó era el Blackjack, con μ = -0,0029036, σ = 1,1417. Su devolución de pérdidas fue L = 20 % y su unidad de apuesta fueron 100.000 $. Reprogramé mi programa para encontrar los valores de x y de b que maximizaran el retorno de Johnson:
|
$ ./BrownianLR -0,0029036 1,1417 .2 100000 |
|
|
% de devoluciones de pérdidas: |
20,0 % |
|
Punto de retirada por pérdidas: |
$2.600.000 |
|
Punto de retirada por ganancias: |
$2.400.000 |
|
Ganancias esperadas: |
$124.999 |
|
Rondas esperadas: |
478,9 |
|
Porcentaje de ganancias: |
49,2 % |
La cifra final en este resultado (porcentaje de ganancias) mostraba el porcentaje de veces que Johnson conseguiría su punto de retirada por ganancias antes de alcanzar su punto de retirada por pérdidas.
En otro post, determiné mediante una simulación que con una retirada tras perder 2.750.000 $ y una tras ganar 2.200.000 $, Don Johnson tendrá unas ganancias previstas de 125.209 $ en 453 rondas. Estas cifras se acercan significativamente a lo que se predijo en teoría.
Ejemplo 2. Baccarat, devolución de pérdidas = 18 %.
Este es otro ejemplo. Imagina que el juego es el Bacará y que el jugador solo está haciendo apuestas de la banca de 100.000 $. En este caso, μ = -0,010579, σ = 0,927372, L = 18 %, con la unidad de apuesta = 100.000 $:
|
$ ./BrownianLR -0,010579 0,927372 .18 100000 |
|
|
% de devoluciones de pérdidas: |
18,0 % |
|
Punto de retirada por pérdidas: |
$400.000 |
|
Punto de retirada por ganancias: |
$400.000 |
|
Ganancias esperadas: |
$18.104 |
|
Rondas esperadas: |
18,6 |
|
Porcentaje de ganancias: |
47,5 % |
En la simulación, el punto de retirada por pérdidas era de 450.000 $ y por ganancias de 360.000 $. En el caso de la simulación, el jugador ganó 18.050 $ en una media de 18,7 manos. La teoría le da al jugador unas ganancias de 18.104 $ en 18,6 manos. De nuevo, estos resultados se asemejan significativamente. La distribución del Bacará es bastante “normal” (es casi tan normal como una distribución discreta de tres eventos)..
La simulación continuará siendo la mejor herramienta para juegos como Video Poker o para apuestas como las apuestas directas en la ruleta. En particular, la reciente devolución del 100 % de la promoción de pérdidas en Revel fue la mejor que una simulación ha ofrecido.
Las apuestas en casinos conforman el escenario perfecto para probar la coincidencia entre la teoría y la realidad. Ya es hora de volver a los últimos años del siglo XX en términos de análisis de devolución de pérdidas en juegos como el Blackjack o el Bacará.
[Agradecimientos. Me gustaría dar las gracias a Michael Shackleford por aportarme las ideas de la distribución a la hora de utilizar estos resultados para Video Poker. También me facilitó los valores para μ y σ que utilizo en el ejemplo n.º 1 de este artículo].


