Pensaba que había terminado mi trabajo sobre devoluciones de pérdidas cuando publiqué el primer teorema de la devolución de pérdidas (LRT1). Entonces, mi perro me dio una buena idea sobre cómo conseguir una estadística cerrada para los puntos de retirada por ganancias y por pérdidas, y funcionó. Esa se convirtió en el segundo teorema de la devolución de pérdidas (LRT2). Ayer se me encendió la bombilla y pensé que solo tenía que introducir los puntos de retirada de LTR2 en LTR1 y resolver la cantidad máxima que un jugador con ventaja puede ganar aprovechándose de una devolución de pérdidas. Esto terminó siendo un lío, pero, aparte de los errores de álgebra que me hicieron volver a empezar unas cuantas veces, era fácil. El resultado recibe el nombre de tercer teorema de la devolución de pérdidas (LRT3).
Este es el tercer teorema de la devolución de pérdidas (haz clic en la imagen para que se expanda):

El denominador del último término del coeficiente de devolución de pérdidas casi me saca de quicio. No es “e” elevado a una potencia. Solo es “e” multiplicado por ese término de aspecto extraño (1 - L) ^ (1 / L). Pero este último término tiene su propia belleza...
Como el valor de L se establece en 0 (en el caso restrictivo), la expresión (1-L)^(1/L) se convierte en 1/e y f(L) se establece en 0, de modo que el máximo de ganancias previsto es de 0. Esto puede intuirse fácilmente. Lo que no es tan fácil es que el valor de L pase a 1 (en el caso restrictivo), f(L) se convierta en 1/e, de modo que,
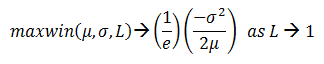
Este es el origen de mi resultado: LRT3_Proof
LRT3 es increíblemente fácil de poner en práctica. El usuario simplemente busca la ventaja de la casa y la desviación estándar del juego en cuestión. Para una determinada cantidad de devolución de pérdidas, el coeficiente de devolución de pérdidas para L puede calcularse con una simple hoja de cálculo. LRT3 produce el número de unidades que ganará el jugador con ventaja (de media) si sigue una estrategia óptima de retirada por ganancias y retirada por pérdidas.
Antes de ofrecer algunos ejemplos, me gustaría hacer hincapié en lo siguiente. Vemos que el máximo de ganancias previsto es directamente proporcional a la varianza (desviación estándar al cuadrado) del juego e inversamente proporcional a la ventaja. A menudo escucharás a un jugador con ventaja afirmando que aumentando la varianza se mejora la devolución potencial mediante el aprovechamiento de la devolución de pérdidas. Esta fórmula lo aclara. Dobla la desviación estándar y multiplica la tasa de ganancias por 4. Dobla la ventaja de la casa y divide a la mitad la tasa de ganancias.
Otro comentario rápido. Unas anotaciones te demostrarán que las ganancias máximas o maxwin > 0, sin importar los valores de las variables por las que se sustituya. Es decir, una consecuencia de LRT3 es que toda promoción de devolución de pérdidas sin restricciones en todo juego de casino puede derrotarse.
La siguiente tabla presenta los coeficientes de devolución de pérdidas para algunos de los porcentajes de devolución de pérdidas más habituales:
|
Devoluciones de pérdidas: Coeficiente |
|
|
Porcentaje de devolución de pérdidas |
Coeficiente |
|
5 % |
0,0003206 |
|
8 % |
0,0008336 |
|
10 % |
0,0013165 |
|
12 % |
0,0019164 |
|
15 % |
0,0030444 |
|
18 % |
0,0044590 |
|
20 % |
0,0055690 |
|
25 % |
0,0089643 |
Aquí tienes algunos ejemplos.
Ejemplo 1. Don Johnson. En su caso:
- μ = -0,0029036
- σ = 1,1417
- L = 0,20
Si observas el 0,20 de la tabla anterior, el coeficiente de devolución de pérdidas es 0,0055690. Por consiguiente, el máximo de ganancias previsto para Don Johnson sería:
maxwin = [(1,1417)^2/(2 x 0,0029036)] x (0,0055690) = 1,250013.
Como la “unidad” para Don Johnson eran 100.000 $, sus ganancias previstas por día eran de 125.001 $.
Ejemplo 2. Ruleta 0 único, apuestas directas de $1.000, devolución de pérdidas del 12 %. En este caso:
- μ = -0,0270270
- σ = 5,8378
- L = 0,12
Si observas el 0,12 de la tabla anterior, el coeficiente de devolución de pérdidas es 0,0019164. Por consiguiente, el máximo de ganancias previsto por aprovechar una devolución de pérdidas del 12 % en apuestas directas en ruletas con 0 único es:
maxwin = [(5,8378)^2/(2 x 0,0270270)] x (0,0019164) = 1,208264.
Como la “unidad” es 1.000 $, el máximo de ganancias previsto por sesión es 1.208 $. Se invita al lector a que calcule las ganancias máximas o maxwin para una ruleta con 0 único para apuestas a pares e impares (σ = 0,9996, mismo μ y L).
Este es un aspecto de los coeficientes de devolución de pérdidas que me gustaría sacar a la luz a modo de ejemplo. Para un juego fijo, una devolución de pérdidas del 10 % utiliza el coeficiente de devolución de pérdidas del 0,0013165, mientras que para una devolución de pérdidas del 20 % utiliza el coeficiente de devolución de pérdidas del 0,0055690. Por consiguiente, las ganancias máximas disponibles de una devolución de pérdidas del 20 % sería (0,0055690/0,0013165) = 4,23 veces el disponible de una devolución del 10 %. Al ofrecer dos veces el porcentaje de devolución de pérdidas se cuadruplica la vulnerabilidad del juego con ventaja.
Aquí se incluye un gráfico del coeficiente de devolución de pérdidas como una función del porcentaje de devolución de pérdidas:
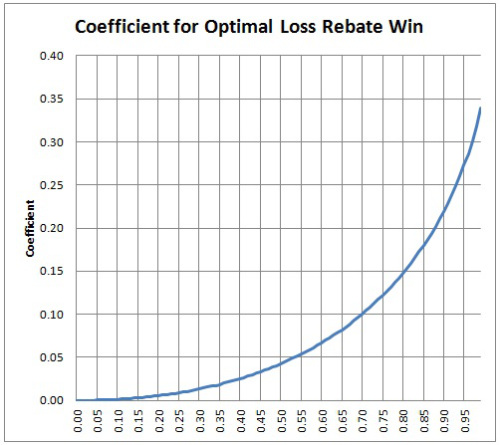
Por el momento, no sé qué más hay que hacer para seguir trabajando en esta dirección en el problema de la devolución de pérdidas. Sacaré a mi perro de paseo más tarde, a ver qué se me ocurre. [Nota. Saqué al perro de paseo. Ni una idea nueva. ¡Perro malo!]


