• El jugador deberá envolver con su mano los dados.  
• Tras un movimiento pendular del brazo, el jugador soltará los dados (dando un revés con el dorso de la mano) y estos dibujarán un arco suave en el aire. 
• El jugador deberá colocarse correctamente y hacer rodar los dados de la forma menos aleatoria posible, tratando de que la trayectoria del lanzamiento responda a su criterio y no al azar. 

Contenido:

• Cómo tirar los dados
• Reglas básicas y tipos de apuesta en el juego de los dados
• Vocabulario del lanzamiento de dados
• El objetivo de cualquier lanzador de dados
• El control del lanzamiento
• Practicar en casa el lanzamiento de dados
• Tirar dados online
• Cómo usar un dado virtual

En este artículo, además de darte algunos consejos prácticos para lanzar bien los dados, queremos explicarte algunos detalles importantes que te servirán para comprender mejor este apasionante juego de casino que, aunque no es muy habitual en los casinos de España, sí cuenta con millones de aficionados en Estados Unidos. En este país está, sin duda, en el top 10 de los juegos de casino más populares. 

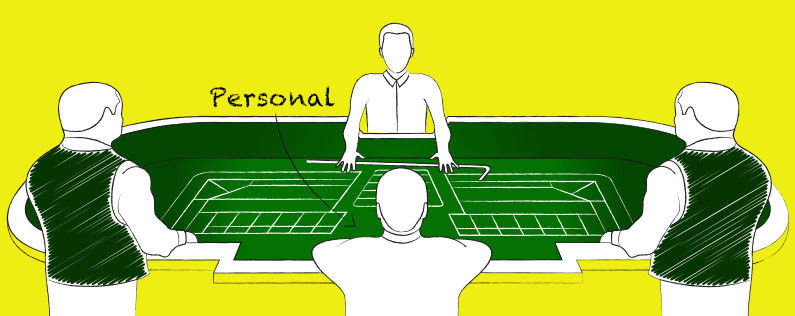
Para saber cómo jugar a los dados necesitamos conocer las distintas reglas, los tipos de apuestas que existen y la forma en la que está organizado el juego. No en vano hablamos de uno de los juegos de casino más complejos que encontraremos tanto en los casinos online como en los presenciales, donde se necesitan de cuatro a cinco empleados para controlar totalmente una mesa de dados.

Sin embargo, en este artículo nos centraremos en uno de los aspectos más importantes de este juego: el lanzamiento. Dicho lanzamiento no depende sólo del azar sino que la habilidad jugará un papel importante. Esto no sucede en otros pasatiempos como las tragaperras online o la ruleta, donde la suerte es el factor fundamental. 

En las siguientes líneas te explicaremos cómo realizar buenos lanzamientos basados en la teoría fundamental que se ha escrito sobre este juego. Un juego de azar que, como tantos otros, ya tiene sus propias versiones virtuales, entre las que se encuentran diferentes webs que ofrecen dados online o videojuegos como Casino GTA.

Para tirar bien los dados y que estos rueden correctamente, será crucial la forma en la que los colocamos en nuestra mano, cómo los sostenemos y cómo nos preparamos para el lanzamiento. 

Te mostramos las claves para ser un buen lanzador de dados: 

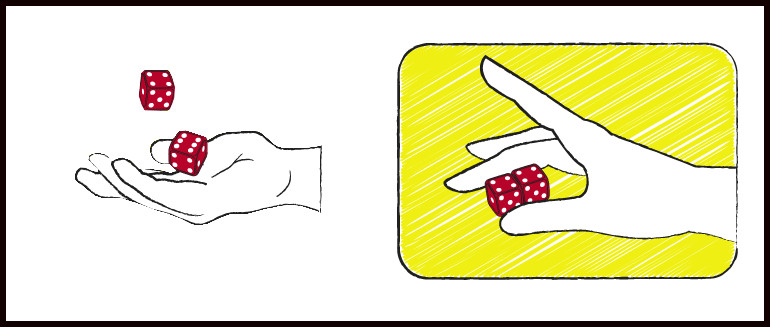
• Envolver los dados

Algunos tiradores envuelven los dados con su mano completa, luego dan un revés, con el dorso de la mano mirando hacia la pared donde va dirigido el lanzamiento. Algunos mueven los dados en su mano, acunándolos entre su pulgar, índice y dedo medio y lanzan los dados hacia el final. La colocación de los dados en nuestra mano, además de mantenerlos ocultos, sirve para garantizar un buen movimiento y una correcta caída de los mismos dentro de la mesa de los dados.

 

• Colocar bien los dados

Pero el método preferido por muchos es colocar los dados uno al lado del otro, bien encajados, luego levantar con el pulgar y el dedo medio a lo largo de la línea entre los dados, de modo que el pulgar toque ambos dados en un lado y en el medio el dedo toque ambos dados en el otro. Luego balancean su brazo completo en un movimiento pendular y sueltan los dados dibujando un arco suave.

 

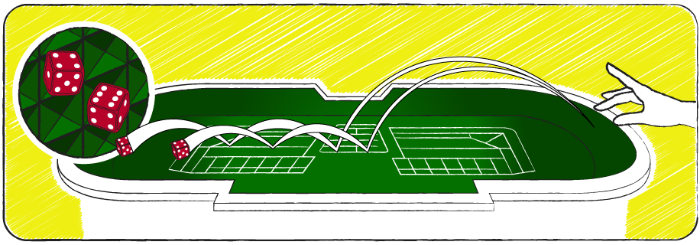
• Lanzamiento al aire 

Como tirador, la regla básica es que debes lanzar los dados al aire. Si el crupier, que es el jefe del equipo de dealers de la mesa de dados que opera el juego, no ve los dados en un arco sobre la mesa, no puede tirar ningún tiro. En ese caso, su tirada no cuenta, y debe tirar nuevamente. 

En tu lanzamiento, los dados deben golpear la pared del fondo al final de la mesa. Si los dados no llegan a golpear la pared del fondo, el boxman no puede tirar ningún tiro.

Las paredes de la mesa generalmente tienen protuberancias en forma de pirámide, diseñadas de modo que en lugar de que los dados reboten de una manera predecible, rebotan en ángulos para aleatorizar el lanzamiento. El relleno debajo del fieltro en la superficie de la mesa varía de un casino a otro. Una superficie que crea más rebote en el rollo ayuda a aleatorizar los resultados.

 

• Colocación del jugador a la hora de lanzar los dados

En primer lugar debes conocer dónde debes colocarte. Cuando un tirador corta, los dados se ofrecen al siguiente jugador en el sentido de las agujas del reloj alrededor de la mesa. Cuando ese jugador corta, los dados pasan al siguiente jugador, y así, sucesivamente, alrededor de la mesa. Cuando sea tu turno, el stickman empujará varios dados hacia ti. El stickman es uno de los miembros del equipo que dirige el juego. Es fácil de detectar porque tiene un palo grande, curvado al final para poder enganchar los dados después de cada lanzamiento y devolverlos al tirador.

 

• Saber hacer rodar los dados

El objetivo básico para un buen lanzamiento es que los dados rueden, pero no sin criterio sino en la forma que hayas decidido. Antes de tirar dados, debes apostar en la línea de pase. Cuando obtienes el visto bueno para rodar, los dados deben hacerlo hacia el final de la mesa.

El principal consejo que podemos darte es que, antes de tirar dados en un casino, practiques un poco en casa; esto ayuda mucho a aliviar cualquier ansiedad que pueda tener un principiante. 

En cuanto a las reglas básicas a tener en cuenta antes del lanzamiento para evitar errores en los dados serían las siguientes:

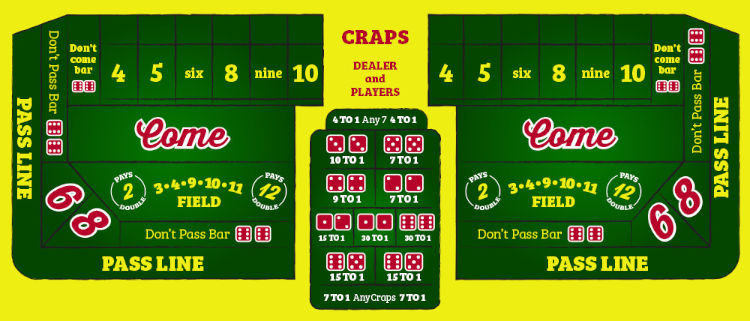
• Línea de pase: tienes que saber cómo funcionan las apuestas y cuándo es tu turno. Hay docenas de apuestas disponibles, pero la línea de pase es fundamental para el juego de dados. Así, por ejemplo, en una apuesta multiroll que comienza con un "rollo de salida"; antes de la salida, los jugadores que quieran apostar en el pase colocan fichas directamente frente a ellos en el área marcada como "línea de pase".
• Apuesta de pase: el tirador debe hacer una apuesta de pase. Si no quieres apostar en el pase, los dados van al siguiente tirador. En la tirada de salida, si la tirada es 7 u 11, los apostadores de pase ganan. Si el resultado es 2, 3 o 12, los números designados como "dados", los apostadores de pase pierden.
• Número de punto: si la tirada de salida es 5. 6. 7, 8, 9 o 10, ese número se designa como el "punto". El distribuidor voltea un disco de plástico a un lado con la etiqueta "on" y lo coloca en el cuadro del número de punto en la mesa. Ahora el objetivo del tirador cambia. Debe lanzar ese número de punto nuevamente antes de sacar un 7. Si repite el número de punto, todos los apostadores de pase ganan, pero si primero saca un 7, todos los apostadores de pase pierden. Una vez que se establece el punto no hay otros números sino 7 y el punto es importante para decidir la apuesta de pase. Otros números podrían decidir otras apuestas que nosotros y otros jugadores hagan, pero el resultado de la apuesta de pase depende del tirador, el número de puntos y 7.
• Siete: perder al sacar un 7 después de que se haya establecido un punto se llama "siete". Solo después de que el tirador corta, los dados pasan a un nuevo tirador. Si el tirador tira un perdedor 2, 3 o 12 en la salida, sigue disparando; esto es válido tanto para lanzar dados en el live casino de internet como en el propio casino presencial. 

Los lanzadores de dados que hay en un casino tienen un lenguaje propio pero, además, los dealers o crupiers constantemente van a utilizar expresiones que, a veces, para el jugador principiante, no son nada comunes. 

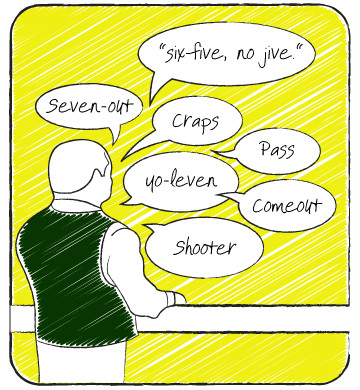
A menudo escucharás expresiones en inglés que suenan como "Yo-leven" o, a veces, simplemente "yo", en referencia al 11; algunos dealers o crupiers también pueden decir "seis y cinco". 

Glosario básico del lanzamiento de dados

• Tirador: el jugador al que le ha llegado el turno de tirar los dados.
• Salida: es el lanzamiento inicial de la secuencia de pase. El crupier generalmente alertará a la mesa de que el próximo lanzamiento es un "call out" diciendo "saliendo" o, en el caso de un cambio de tirador, "nuevo tirador saliendo".
• Pase: un área entre dos líneas que se extienden alrededor de la mesa se llama "línea de pase". Una apuesta realizada en esa área es una apuesta de pase, como se describió anteriormente en este capítulo. Si el tirador hace un punto y los apostadores ganan, se dice que el tirador hizo un pase.
• Craps: los rollos de 2, 3 o 12 se llaman "craps" y son perdedores en la línea de pase si salen al salir.
• El punto: el número que el tirador debe tirar antes de las 7 para hacer un pase. Eso se determina si la tirada de salida es 4, 5, 6, 8, 9 o 10; ese número se designa como el punto.
• Siete fuera: perder una apuesta de pase tirando un 7 antes de repetir el punto.

Debes obedecer todas las reglas de la mesa. Debes poner suficiente arco en tu rollo para satisfacer al boxman y tu rollo debe golpear la pared del fondo.

Sin embargo, las tiradas calientes que hacen dinero para los jugadores generalmente implican una racha en la que el tirador tira menos 7 segundos de lo habitual. Menos 7 significa más puntos hechos antes del siete out.

Cómo lanzar dados: tu objetivo como tirador será ganar con 7s en las tiradas de salida, pero para los jugadores que respaldan sus apuestas de pase con probabilidades libres, las grandes victorias se obtienen al hacer los puntos. Y no puedes hacer los puntos cuando los dados siguen cayendo en 7.

En los buenos tiempos, pareces entrar en un ritmo en el que los números de puntos están rodando y los 7 son pocos y distantes entre sí. La pregunta que los jugadores de dados se han estado preguntando durante siglos es si hay algo que puedan hacer para que los buenos tiempos lleguen con más frecuencia.

Ya sea que esté apostando solo en la línea de pase o en otras apuestas, no se necesita mucha desviación de la norma para cambiar la ventaja de la casa a favor de los jugadores.

Haga las apuestas de lugar en 6 u 8, como se describió anteriormente. Cuando los 7 ocurren un promedio de una vez cada seis tiradas, como lo hacen en un juego aleatorio, la casa tiene una ventaja de 1.52 por ciento: por cada $100 apostados, la casa espera mantener $1.52.

Pero, ¿qué pasa si los 7 no aparecen una vez cada seis rollos? ¿Qué pasa si el tirador tiene un método que suprimirá los 7 segundos para que aparezcan con menos frecuencia?

Algunos estudios han calculado que un tirador alcanza el punto de inflexión, tomando una ligera ventaja cuando puede reducir la frecuencia de 7s a 1 en 6.1428. Disminuye la frecuencia a 1 en 7, y los jugadores que apuesten 6 y / u 8 obtienen una enorme ventaja de 8.333 por ciento sobre la casa. Que la brecha de 1 en 6 rollos a 1 en 6.1428 sea estrecha no lo hace fácil. Pero aquellos que practican el control de dados dicen que pueden llegar allí.

Este pasatiempo no es uno de los juegos tradicionales de España ni está entre los más populares, así que es posible que no sepas que cuando hablamos de control no nos referimos a tirar números específicos. Nadie afirma ser capaz de subir a la mesa para lanzar 6 a voluntad, o cualquier otro número.

La mayor parte del énfasis está en disminuir la proporción de 7 una vez que se ha establecido un punto. Algunos jugadores que pasan al siguiente nivel también intentan aumentar la proporción de 7s en la salida, por lo que ganan con más 7s en la salida y también con menos 7s después de que haya un punto.

El método para hacerlo suena fácil, pero tenga en cuenta que esta es una habilidad física. Al igual que otras habilidades físicas, como lanzar tiros libres en baloncesto, jugar bolos o jugar al billar, el control de dados requiere mucha práctica y memoria muscular.

No todos los que lo prueben podrán ponerlo en práctica y obtener una ventaja sobre la casa. Algunos jugadores, tal vez incluso la mayoría de los jugadores, descubrirán que nunca pueden cruzar el puente a partir de resultados aleatorios.

En teoría, todo suena bastante fácil en cuanto a la mecánica: balancea el brazo pendularmente y suelta los dados con suavidad para que reboten un número mínimo de veces. En la práctica, es una habilidad física difícil que lleva tiempo dominar. Los expertos en control de dados sugieren que se reserve hasta una hora al día para practicar la tirada. 

La simulación más fiel a un casino real es la de una mesa de dados reglamentarios; lo ideal es practicar con ella. Hay varios problemas con ese método. Por un lado, en algunas jurisdicciones, la propiedad privada de los equipos de juego es ilegal. Incluso donde es legal, las mesas de dados son caras y ocupan mucho espacio, por eso es mejor buscar mesas gratuitas en casinos online. Evidentemente ahí no podremos practicar el lanzamiento físico, pero sí los turnos, las rondas de apuestas, el léxico y, sobre todo, comprenderemos qué está pasando en cada lanzamiento, ya sea nuestro turno o no.

Actualmente, casi todos los juegos de casino tienen su propia versión virtual, de modo que podemos jugar al blackjack online o al poker desde nuestra propia casa, a través de un casino móvil y mediante cualquier dispositivo digital. El juego de los dados no es una excepción; con sólo buscar un poco encontraremos decenas de webs donde tirar dados online. Usaremos estos dados virtuales sin necesidad de descargar ninguna aplicación, directamente con nuestro navegador. 

Pero, ¿qué nos ofrece un dado virtual? y, ¿para qué querríamos usarlo? Bueno, la respuesta más sencilla es que puede darse el caso de que estemos jugando a un juego de rol o a cualquier juego mesa y no disponer, por la razón que sea, de un dado físico. Una forma de resolverlo fácilmente es acudiendo a estos dados para tirar online a través de nuestro móvil, PC o tablet. Los dados, ya sean físicos o virtuales, se utilizan para generar números aleatoriamente; estos objetos son herramientas fundamentales para muchos juegos de mesa y algunos juegos de azar en los que el propio dado es el protagonista principal. 

¿Qué es un dado?

Los dados virtuales emulan los dados físicos “reales” y reproducen todas sus funciones. El dado físico consiste en un objeto tridimensional que, usualmente, tiene forma cúbica y dispone de 6 caras (d6) aunque los hay de muchas formas (no cúbicas) y con un número variable de caras. Estos dados, menos frecuentes, se suelen usar en juegos de rol. En cada una de las caras del dado vendrá señalado un número (o símbolo) que indicará el valor de cada lanzamiento. 

El dado virtual o dado online

El dado virtual es una simulación de dado que usaremos a través de una web o aplicación, las cuales podemos configurar para que tenga el número de caras y, en ocasiones, la forma concreta que deseemos. 

Funcionamiento de un dado virtual

Para aprender a usar un dado online tomaremos como ejemplo el que nos ofrece la web dado.online. De todos modos, casi todas las aplicaciones o páginas que ofrecen dados virtuales personalizables (app-sorteos.com, dado-virtual.com, piliapp.com, entre otras) funcionan de igual o muy similar manera. 

• Número de dados: el primer paso que daremos será elegir el número de dados que necesitamos; podremos elegir hasta un máximo de 6, además de disponer del modo “cualquier” en el que la web, aleatoriamente, decide la cantidad. 
• Número de cara: en el menú desplegable situado a la derecha de la pantalla podemos elegir el número de caras (hasta un máximo de 100) o bien, como ocurre en el punto anterior, seleccionar el modo “cualquier” y dejar que el software, de modo arbitrario, elija por nosotros. También se puede elegir el modo fudge que corresponde con tipo especial de dados usado en determinados juegos.
• Lanzamiento: para iniciar el lanzamiento deberemos clicar en la palabra tirar o bien, desde el teclado de nuestro ordenador, en la tecla enter. 
• Resultado: una vez hemos elegido el número de dados, el número de caras y hemos clicado en tirar, el software generará, aleatoriamente, el resultado. En el caso de que hayamos lanzado varios dados a la vez, dicho resultado será la suma de los mismos. 

Fuente: Youtube

 

Aviso: Todos los consejos dados en este artículo tienen un carácter meramente informativo basado en bibliografía sobre juegos de azar. Sin embargo ninguno de estos consejos garantiza ni es un elemento determinante para el éxito en la actividad del juego analizado. En nuestro blog tratamos temáticas relacionadas con el mundo de los juegos y los contenidos son informativos y no significa que tengamos disponible el juego, producto, utensilio, accesorio, etcétera…del que habla el artículo.

• Con jugadas de ruleta nos referimos a aquellas estrategias y apuestas que podemos realizar con el objetivo aproximarnos a la victoria
• Entre las estrategias de ruleta más conocidas encontramos la Martingala, el sistema D’Alembert y la secuencia Fibonacci
• En la ruleta europea, algunas de las apuestas más populares son Huérfanos, Vecinos del cero, Juego del cero o Tercio  
   

Todos los juegos de casino dependen, en última instancia, del azar. Sin embargo, no todos lo hacen en la misma medida: los jugadores de slots online sólo pueden tratar de conocer a fondo el juego y, al final, entregarse a la suerte; los jugadores de roulette, en cambio, tienen más opciones, ya que es un juego que permite la aplicación de determinadas estrategias que aumentan nuestra ventaja y nuestras probabilidades en la ruleta. 

Si queremos saber cómo ganar en la ruleta, tanto en un casino online como en uno offline, debemos tener una mínima aproximación estratégica; debemos, desde luego, conocer bien las reglas de ruleta, las diferentes apuestas que podemos realizar, los sistemas que podemos aplicar y, en definitiva, las mejores jugadas ruleta que podemos llevar a cabo.

De todo eso hablaremos en el artículo de hoy. 

Las jugadas de ruleta: qué son

Una jugada de ruleta es una apuesta realizada por un jugador, donde se intenta predecir el resultado del giro de la rueda. Estas apuestas pueden variar en términos de números específicos, combinaciones de números, colores o características de grupos de números en la mesa de juego.

Las jugadas de ruleta son también aquellas que se efectúan cuando aplicamos las estrategias de ruleta más populares. Estos sistemas de ruleta, como ya hemos explicado en otras ocasiones, no son perfectos ni garantizan nuestro éxito, pero sí dan un poco más de sentido a nuestras apuestas y jugadas de ruleta. 

Afortunadamente, los juegos online nos permiten poner en práctica, gratuitamente, todas las jugadas de la ruleta que deseemos, de modo que iremos viendo cuáles de ellas nos convienen, por nuestra forma de juego, nuestro bankroll, etc. 

Mediante la ruleta demo podremos aplicar nuestras estrategias de ruleta preferidas, nuestras mejores jugadas ruleta e ir perfeccionando nuestras habilidades hasta que nos sintamos seguros para apostar. 

Si lo tuyo son las tragaperras con dinero real o el blackjack online de casino; no te preocupes, también encontrarás demo slots y varios tipos de simulador de blackjack con los que podrás hacer lo mismo. 

Veamos ahora las 3 jugadas ruleta más famosas.

Mejores jugadas ruleta: sistema Martingala

La Martingala es la estrategia de ruleta europea y americana más conocida y sencilla de entender. Es uno de los sistemas para ganar en la ruleta más usados. Se trata de apostar una cantidad fija –no necesariamente elevada– en una apuesta de suerte sencilla del tipo rojo/negro, par/impar o falta/pasa. En caso de perder la apuesta, en la siguiente bola doblamos la apuesta, y así sucesivamente. Si ganamos, volvemos a la apuesta inicial, pero si perdemos tenemos que doblar nuevamente la anterior apuesta. 

Sin embargo, hay un problema con este método: los casinos tienen unos límites de apuesta máxima para tratar, precisamente, de contrarrestar esta conocida estrategia de la Martingala. 

Vamos a explicar un poco más este tipo de estrategia con un ejemplo concreto:

Estamos en un casino en vivo en una mesa de ruleta francesa de 2€ y tenemos un presupuesto de 1,000€. 

• Paso 1: Apostamos 2€ al rojo. Cae rojo, por lo que ganamos 2€ (nos pagan 4€ pero habíamos invertido 2€). Aquí tenemos la opción de repetir al rojo o cambiar al negro, es indistinto. Saldo neto: +2 €. Supongamos que seguimos en el rojo. 

• Paso 2: Apostamos 2€ al rojo. Cae negro, por lo que perdemos 2€. Saldo neto: 0

• Paso 3: Apostamos 4€ al rojo. Cae negro de nuevo, y perdemos otros 4€. Saldo neto: -4

• Paso 4: Apostamos 8€ al rojo. Esta vez cae rojo, y nos pagan 16€ (pero habíamos puesto 8€), con lo que la ganancia neta en esta jugada es +8. Saldo neto: +4. 

Con la estrategia de la Martingala, ganaremos x * y, donde “x” es el tamaño de la apuesta inicial e “y” es el número de aciertos consecutivos. Por ejemplo, en esta mesa, después de 50 aciertos habremos ganado: 2*50= 100 € netos. 

Fuente: Youtube

Mejores jugadas ruleta: estrategia d´ Alembert

Este sistema es mucho menos arriesgado que el anterior, ya que no tenemos que doblar las apuestas que perdemos sino añadir una unidad más de apuesta. 

Podemos ejemplificar esta estrategia utilizando nuevamente el caso de una mesa de ruleta francesa con una apuesta mínima de 2 euros:

• Paso 1: Apostamos 2€ al par y cae impar. Perdemos 2€.
• Paso 2: Apostamos 2 veces lo anterior, es decir 4€ y también perdemos. Saldo neto: -6€.
• Paso 3: Apostamos 3 veces la apuesta mínima, es decir 6€ (recordad que en Martingala aquí deberíamos apostar el doble de lo anterior, en este caso 8€). Ganamos y recuperamos las pérdidas anteriores. Saldo neto: 0
• Paso 4: Apostamos la apuesta mínima y ganamos. Saldo neto: +2€. 

Con esta estrategia, si acertamos tantas veces como fallamos, nos mantenemos en equilibrio, lo que se conoce como "break even". Esto implica un menor riesgo de pérdida total, ya que es menos probable alcanzar el límite máximo de apuesta en la mesa. Sin embargo, las ganancias potenciales son menores en comparación con la estrategia de la Martingala.

Desde el punto de vista matemático podemos decir que, usando d’Allembert, las ganancias se traducen en la fórmula siguiente: (número de aciertos – número de fallos) * tamaño mínimo de apuesta. Supongamos que después de 100 bolas, hemos acertado 53 y perdido 47. Nuestras ganancias serán de: (53-47)*2= 12€. 

Fuente: Youtube

Mejores jugadas ruleta: sistema Fibonacci

En esta estrategia de juegos de casino, el jugador aumenta o disminuye su apuesta siguiendo la secuencia de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, etc. Cada número es la suma de los dos anteriores. Si pierde, avanza un paso en la secuencia; si gana, retrocede dos pasos.

Detengámonos en la secuencia: 1-1-2-3-5-8-13-21-34-55-89-144-233-377-610-… Es decir, empezamos con el 1, seguimos otra vez con el 1 (porque 1+ nada= 1) y a partir de ahí, 2 (es la suma de 1+1), 3 (es la suma de 2+1), y así sucesivamente. 

¿Cómo aplicar esta estrategia a la ruleta? En este caso, si cosechamos una serie de resultados negativos deberemos primero multiplicar la apuesta x1; x2 en el siguiente intento; x3 en el tercero; x5 en el cuarto; x8 en el quinto; y continuamos de ese modo, siguiendo siempre la secuencia Fibonacci. 

Vamos a utilizar el mismo ejemplo que con las dos anteriores estrategias: 

• Paso 1: Apostamos 2€ a falta (comprende los números del 1 al 18). Ganamos. Saldo neto: +2€. 

• Paso 2: Apostamos 2€ a falta. Perdemos. Saldo neto: 0

• Paso 3: Apostamos de nuevo 2€ (porque el segundo número de la serie es 1 así que multiplicamos la apuesta por 1 de nuevo: 2€*1=2€). Perdemos. Saldo neto: -2€. 

• Paso 4: Apostamos 4€ (2€*2=4€). Perdemos de nuevo. Saldo neto: -6€. 

• Paso 5: Apostamos 6€ (2€*3= 6€). Perdemos de nuevo. Saldo neto: -12€. 

• Paso 6: Apostamos 10€ (2€*5=10€). Ganamos. Saldo neto: -2€. 

Con esta estrategia, a diferencia de las dos anteriores, no conseguimos recuperarnos totalmente de las malas rachas, pero al menos no arriesgamos doblando cada vez la cantidad apostada. 

Frame - Fuente: Youtube

Ruleta jugadas prohibidas 

Para finalizar esta sección debemos aclarar una cuestión: con frecuencia se dice que hay una serie de ruleta jugadas prohibidas, y se pone como ejemplo, en ocasiones, a La Martingala. Debemos saber que esto no es cierto. El jugador podrá aplicar las jugadas de la ruleta que crea convenientes, siempre que estas no contradigan las reglas del juego. Las ruleta jugadas prohibidas son mucho más un mito que una realidad. 

Jugadas ruleta: los tipos de apuesta más populares

Son muchas las jugadas de ruletas que podemos hacer. A continuación enumeramos y explicaremos algunas de las apuestas en la ruleta más relevantes. Todas ellas son propias de la ruleta europea o la ruleta francesa; es decir, aquellas que tienen un sólo cero (0). O bien de la variante de la ruleta americana que no dispone de doble cero (00).

• Huérfanos: Esta apuesta cubre un total de 8 números que no están incluidos en las otras apuestas principales. Los jugadores tienen dos opciones para realizar esta apuesta: pueden hacerla con apuestas a "caballo" o con apuestas a "pleno".

• Huérfanos con apuestas a caballo: esta apuesta se realiza con 5 fichas y consiste en apostar a un total de 8 números huérfanos con apuestas a caballo. Debido a cómo están ubicados los números huérfanos en el tapete, no es posible cubrirlos todos solamente con apuestas a caballo (apuestas en dos números contiguos). Por lo tanto, para asegurar que todos los huérfanos estén cubiertos, se realiza una apuesta plena en el número 1 (ya que este no está cubierto por ninguna apuesta a caballo). Además, el número 17 se cubre con dos apuestas a caballo, ya que es vecino tanto del número huérfano 20 como del 14.

• Huérfanos con apuestas a pleno: en esta jugada de ruleta se apuesta en un conjunto de 8 números utilizando 8 fichas. La estrategia denominada "apuesta huérfanos con apuestas pleno" implica realizar una apuesta plena en cada uno de los números huérfanos.

• Vecinos del cero: Esta apuesta cubre un grupo de 17 números en la ruleta que rodean al cero, y el propio cero. Para realizar esta apuesta, se colocan 9 fichas en una sección específica de la mesa de ruleta. 

• El cero y sus vecinos: en los casinos de España es bastante habitual que los jugadores añadan una ficha extra a la apuesta de Vecinos del cero. La apuesta resultante es conocida como El cero y sus vecinos y consistirá, por tanto, en apostar con 10 fichas a un grupo de 17 números.

• Tercio: en esta apuesta apostamos a un grupo de 12 números (que conforman el tercio de la rueda) mediante 6 fichas. A esta apuesta se le llama también “serie pequeña”. 

• Vecinos de un número: dentro de las jugadas de ruleta que podemos realizar está la de “Vecinos de un número”. Esta apuesta consiste en apostar a un número y a los números adyacentes a este (o vecinos).  

• Juego de 0: en este caso apostamos a los dos números que quedan del lado derecho del 0 (32 y 15) y a los 4 que quedan a su izquierda (12, 35, 3 y 26). 

• Juego de 0 + 19: se trata de una variación de la apuesta anterior. En este caso añadimos una ficha en el lado izquierdo, apostando un pleno en el número 19. Ahora tendremos 4 números a la derecha del cero y 3 a su izquierda. 

Estas son algunas de las mejores apuestas de ruleta; si quieres llegar a ser un experto, estúdialas con paciencia y dedicación.

 

Aviso: Todos los consejos dados en este artículo tienen un carácter meramente informativo basado en bibliografía sobre juegos de azar. Sin embargo ninguno de estos consejos garantiza ni es un elemento determinante para el éxito en la actividad del juego analizado. En nuestro blog tratamos temáticas relacionadas con el mundo de los juegos y los contenidos son informativos y no significa que tengamos disponible el juego, producto, utensilio, accesorio, etcétera…del que habla el artículo.

• En las mesas de juego, las fichas de casino sustituyen al dinero en efectivo

• No todas las fichas son iguales: su diseño y uso dependen del juego y del tipo de mesa

• Existen fichas con valor impreso, fichas de color y placas para apuestas altas

 

Los jugadores reconocen cada detalle cuando entran en un casino: la emoción contenida en las mesas de blackjack, los crupieres cantando los números de ruleta, el sonido de los dados rodando sobre el tapete… Todos los elementos son familiares e importantes para el aficionado. Y aquí incluimos, cómo no, las fichas de casino. 

De ellas hablaremos hoy largo y tendido. Si te gustan las historias de casino, no te lo pierdas. 

Fichas de casino: qué son, cómo funcionan y por qué son importantes

Las fichas de casino son uno de los elementos más reconocibles del mundo del juego. Más allá de su estética o de su valor simbólico, cumplen una función esencial: sustituir el dinero en efectivo en las mesas y facilitar el desarrollo de los juegos de azar con seguridad y fluidez.

En cualquier casino presencial, el proceso es el mismo: el jugador cambia su dinero por fichas en la caja o directamente en la mesa. A partir de ese momento, todas las apuestas se realizan con ellas, ya sea en la ruleta, en el blackjack o en otros juegos de casino.

En el entorno digital ocurre algo distinto. En un casino online, las fichas son virtuales, una representación gráfica del saldo del jugador. No tienen existencia física, pero cumplen la misma función: indicar cuánto se apuesta y cuánto se puede ganar.

Pero ¿por qué no se usa directamente dinero en metálico en las mesas? Pues porque:

• Agilizan el juego.

• Facilitan el recuento por parte del crupier.

• Permiten identificar apuestas con claridad.

• Refuerzan la seguridad del establecimiento.

Sin las fichas, el ritmo del juego sería mucho más lento y el control del dinero mucho más complejo.

Materiales, peso y seguridad: cómo se fabrican las fichas de casino

Aunque popularmente se habla de “fichas de arcilla”, lo cierto es que la mayoría de las fichas profesionales actuales no están fabricadas con arcilla pura. Desde mediados del siglo XX se producen mediante compuestos moldeados por compresión que combinan arcilla con otros materiales como carbonato cálcico, tiza, arena fina y distintos aglutinantes o resinas. El resultado es una mezcla más resistente, duradera y adecuada para el uso intensivo en las mesas de juego.

También existen fichas de:

• Cerámica, muy utilizadas en determinados casinos y torneos.

• Plástico, habituales en partidas domésticas, pero no en salas profesionales.

Peso y medidas de las fichas de casino

Las fichas utilizadas en casinos físicos suelen pesar entre 8,5 y 11,5 gramos, aunque esto puede variar según el fabricante. El diámetro estándar ronda los 39 mm.

El peso no es casual. Está pensado para que:

• Se puedan apilar con estabilidad.

• Resulten cómodas al manipular.

• Ofrezcan una sensación sólida y profesional.

Las fichas de casino como sistemas de seguridad

La seguridad es uno de los aspectos más importantes. Las fichas profesionales incluyen:

• Diseños complejos y exclusivos.

• Insertos de colores difíciles de replicar.

• Tintas especiales.

• En algunos casos, tecnología RFID en fichas de alto valor para control interno.

Además, las fichas solo tienen valor dentro del casino que las emite. No valen para todos los casinos de España: cada uno tiene las suyas.

 Fuente: Youtube

Tipos de fichas de casino según el juego

No todas las fichas funcionan igual. Su diseño y uso pueden variar dependiendo del tipo de juego.

Fichas con valor impreso

Son las más comunes. Indican claramente su denominación (1 €, 5 €, 25 €, etc.) y pueden utilizarse en distintos juegos dentro del mismo casino.

Se ven habitualmente en:

• Blackjack

• Poker cash

• Mesas de ruleta estándar

En el blackjack, por ejemplo, el pago habitual por obtener un 21 natural es 3:2. Es decir, si apuestas 10 €, cobras 15 € de beneficio más tu apuesta inicial. Para que esos pagos sean rápidos y exactos, los valores de las fichas están pensados para facilitar las combinaciones.

Si estás aprendiendo cómo jugar al blackjack, entender el valor de las fichas y su equivalencia es fundamental.  Lo mismo ocurre en el póker.  
 

Fuente: Youtube

Fichas de color (sin valor impreso)

Se utilizan sobre todo en la ruleta francesa y en otras variantes europeas. En este caso:

• Cada jugador recibe un color distinto.

• Las fichas no llevan valor impreso.

• El valor lo determina la mesa (por ejemplo, 2 € por ficha).

Este sistema evita confusiones cuando varios jugadores apuestan al mismo número. Todas las fichas permanecen en la mesa hasta que el jugador decide retirarse.

Si te interesa saber cómo ganar en la ruleta, conviene empezar por entender cómo funciona la mesa, qué significan las fichas y cómo se gestionan las apuestas. Ninguna variante elimina la ventaja matemática del casino, pero conocer bien las reglas y la mecánica del juego evita errores innecesarios.

Fichas en torneos de póker

En competiciones de póker de casino, las fichas no representan dinero real directamente, sino puntos de torneo. Un buy-in de 100 € puede traducirse, por ejemplo, en 20.000 puntos repartidos en fichas de diferentes valores.

A diferencia de las partidas con dinero real, aquí las fichas no se pueden cambiar por efectivo: solo indican la posición del jugador en el torneo.

Colores, valores y curiosidades sobre las fichas de casino

¿Existe un código universal de colores en las fichas de casino? La respuesta es no. Aunque muchos casinos siguen patrones similares, no hay una normativa internacional obligatoria.

Sin embargo, es frecuente encontrar:

• Blanco: 1

• Rojo: 5

• Verde: 25

• Negro: 100

• Morado: 500

En cualquier caso, antes de apostar debemos comprobar en la propia mesa cuál es el valor asignado a cada ficha.

¿Qué son las placas?

En mesas de apuestas altas aparecen las llamadas placas. Son similares a fichas, pero:

• Tienen forma rectangular.

• Representan valores elevados.

• Se utilizan en mesas con límites altos.

Son habituales en mesas de casino high roller (tanto de blackjack como de ruleta), donde las apuestas pueden alcanzar cifras importantes.

Fichas y coleccionismo

Las fichas también se han convertido en objetos de colección. Muchos aficionados las guardan como recuerdo de los casinos visitados. Algunos establecimientos incluso lanzan ediciones conmemorativas.

Las fichas de casino forman parte de la memoria sentimental de los jugadores. Cada ficha les recuerda una partida, un casino y una ciudad.

Preguntas y respuestas sobre las fichas de casino

¿Qué son las fichas de casino?  
Son pequeños discos utilizados en las mesas de juego que sustituyen al dinero en efectivo. Representan un determinado valor y permiten realizar apuestas de forma más ágil y segura.

¿Qué tipos de fichas de casino hay?  
Existen fichas con valor impreso, válidas para distintos juegos, y fichas de color sin valor visible, habituales en la ruleta. También hay fichas específicas para torneos y placas rectangulares para apuestas elevadas.

¿Qué juegos de casino utilizan fichas?  
Se utilizan en la mayoría de juegos de mesa como la ruleta, el blackjack y el póker. 

¿Dónde se cambian las fichas?  
En la caja principal del casino o directamente en determinadas mesas. Al terminar la sesión, se vuelven a canjear por dinero en efectivo.

¿Puedo usar fichas de un casino en otro?  
No. Solo tienen validez en el establecimiento que las emite.

¿Por qué en la ruleta cada jugador usa un color distinto?  
Para evitar confusiones cuando varios jugadores apuestan al mismo número.

¿Existen fichas en los juegos online?  
Sí, fichas de casino virtuales. No en todos los juegos, claro: las slots, por ejemplo, no funcionan con fichas.  

 

Aviso: Todos los consejos dados en este artículo tienen un carácter meramente informativo basado en bibliografía sobre juegos de azar. Sin embargo ninguno de estos consejos garantiza ni es un elemento determinante para el éxito en la actividad del juego analizado. En nuestro blog tratamos temáticas relacionadas con el mundo de los juegos y los contenidos son informativos y no significa que tengamos disponible el juego, producto, utensilio, accesorio, etcétera…del que habla el artículo.

• No hay fórmulas mágicas ni estrategias infalibles para ganar a la slots, pero sí podemos aplicar una serie consejos muy útiles
• Es conveniente jugar gratis y familiarizarnos con el juego antes de apostar con dinero real
• Conocer al detalle las características de la slot, aumentar paulatinamente nuestras apuestas, fijar un presupuesto y evitar el juego automático son algunos de los consejos que desde 888casino recomendamos seguir 

 

Las máquinas tragamonedas viven una nueva edad de oro desde la irrupción de las plataformas de juegos online. Slots de todos los tipos y temáticas posibles están a disposición de los jugadores con apenas un clic, y estos buscan las mejores maneras de jugar y de conseguir el anhelado bote. No hay fórmulas mágicas y sabemos que la suerte es el factor determinante, pero sí podemos seguir una serie de consejos con el fin de descubrir cómo ganar en el casino online y, en concreto, cómo ganar en las tragaperras. Quédate con nosotros; el artículo de hoy puede serte tremendamente útil. 

Aprovecha las promociones y juega gratis

Los casinos online de España suelen ofrecer diversas promociones para todos aquellos usuarios que se hayan abierto una cuenta en la plataforma (aquí te explicamos cómo hacerlo en nuestro casino: 888.es login). 

Estas promociones nos dan la oportunidad de jugar gratis a la ruleta o a diferentes tragamonedas online. Además, al registrarte puedes beneficiarte de un casino online bono bienvenida, ideal para empezar a jugar con un extra y probar más títulos sin arriesgar tanto desde el inicio. Mediante el modo “práctica”, es decir, el modo gratuito, podremos familiarizarnos con el juego en cuestión y aplicar, sin ningún riesgo, todos los trucos y estrategias que veamos convenientes. Cuando ya controlemos la mecánica del juego, será hora (si lo deseamos) de lanzarnos a jugar a tragaperras con dinero real. 

No existen las sistemas perfectos

Los sistemas y estrategias están para ayudarnos a aumentar nuestras opciones de éxito y disminuir la ventaja natural del casino. Pero no hay fórmulas mágicas que nos descubran cómo ganar en tragaperras, de la misma manera que no hay un sistema de ruleta infalible con el que ganar a la ruleta americana o europea. 

Además, las slots dependen aún más de la suerte que otros juegos de azar –como el blackjack–, de modo que para tratar de llevarnos el premio, lo único (y es mucho) que podemos hacer es estudiar a fondo el juego. Igual que debemos aprender cómo jugar a la ruleta, deberemos estudiar la mecánica de juego de la tragaperras que hayamos elegido, conocer sus pagos, sus elementos principales y estar muy atento al desarrollo de la partida.

Conoce los pagos

De la misma manera que otorgamos una importancia capital a la RTP de las slots (más adelante lo veremos), debemos atender a sus pagos. Son muchos los casinos que facilitan esa información, de modo que con apenas un click podremos saber cuál es la tragaperras online que ha dado los premios más altos. 

Cuidado con las tragaperras progresivas 

Para entenderlo fácilmente: en las slots “normales”, los jugadores optan a un bote máximo predeterminado. A este premio tienen acceso (potencialmente) todos los jugadores todas las veces. Las tragaperras progresivas, sin embargo, aumentan el valor de sus premios cada vez que un jugador realiza una apuesta (cogiendo un pequeño porcentaje de esta y aumentando el bote común); estamos, pues, ante un premio acumulativo. El bote de las tragaperras progresivas elevará su valor sin límite, hasta que uno de los jugadores se lo lleve. 

Como vemos, las slots con jackpot progresivo pueden hacernos ganar más dinero, pero también conllevan un mayor riesgo: las opciones son más escasas, podemos fácilmente perder el control y para optar al premio máximo debemos también realizar la apuesta máxima posible. 

Si ganas, cambia de slot

Es poco probable ganar varias veces seguidas (o en un corto espacio de tiempo) en el mismo juego de azar, así que nuestra recomendación es que, si te llevas el premio en una determinada slot, cambies de título en la siguiente apuesta. Como ya sabes, hay innumerables tipos de slots, con mecánicas y temáticas para todos los gustos, así que refréscate, prueba otra tragaperras y vuelve pasado un tiempo prudencial. Este consejo cobra más sentido si cabe si nos referimos a las slots progresivas, ya que cuando su premio es otorgado, automáticamente vuelve a valor cero: nos llevaríamos, incluso ganando, un premio de poco valor, así que espera a que el bote acumulativo haya crecido lo suficiente ante de volver a apostar. 

Escoge la tragaperras con mejor RTP

Lo primero, una aclaración: RTP es el acrónimo de Return to Player. En español: tasa de retorno al jugador. Este término se refiere al porcentaje de recuperación del dinero apostado por los jugadores en un determinado juego, y se calcula siempre a largo plazo. Es un valor a tener muy en cuenta, y siempre aparece en la información principal sobre cada juego. 

Las tragaperras online tienen aproximadamente una tasa de retorno al jugador (RTP) mucho más elevada que las tragaperras físicas (hasta un 40% mayor), por lo que las primeras serán siempre una mejor opción si lo que buscamos en mayor probabilidad de ganancias. La RTP, como decimos, mide en porcentajes los beneficios, de modo que lo más habitual es elegir slots con tasas altas, al menos del 96%. 

Mejor una volatilidad alta o media-alta

La volatilidad de una slot va a medir la frecuencia y el valor de los premios que otorga. Si elegimos una tragaperras de volatilidad baja significa que (potencialmente) ganaremos más premios, pero de menor valor. Una slot de volatilidad media-alta nos otorgará premios de mayor valor pero a una menor frecuencia. 

Aumenta poco a poco tu apuesta

Antes de realizar apuestas más elevadas, y a fin de conocer a fondo el mecanismo de juego de una tragaperras, empezaremos apostando la mínima cantidad posible. De ese modo minimizaremos de entrada los riesgos en caso de perder. Ten paciencia; cuando hayas duplicado tus beneficios estarás en posición de elevar tu apuesta. Lo haremos poco a poco hasta llegar a la apuesta máxima que nos permita el juego y el casino. De ese modo optamos también al mayor premio posible. Pero siempre juega y apuesta en función de tu presupuesto, nunca inviertas más de lo que te puedas permitir perder. 

Recuerda que, como hemos mencionado antes, siempre está la opción de jugar gratis; nos servirá de entrenamiento y afianzamiento de nuestro juego.

Fija un presupuesto antes de jugar

Para evitar males mayores, los jugadores deben fijar un presupuesto siempre antes de empezar a jugar. Y las ganancias no deben incluirse en él. Estas no deberían reinvertirse en próximas sesiones: lo ideal es fijar un límite y ceñirse a él rigurosamente. 

Evita el juego automático

Una premisa básica que nos sirve para todos los juegos online de casino: debemos ser prudentes. Y no sólo, debemos estar atentos al juego, controlar con detalle todo cuanto ocurre en la partida y cuánto estamos apostando en cada momento. En definitiva, debemos ser dueños de nuestro juegos y evitar así pérdidas irreparables. Por todo ello no recomendamos activar el modo de juego automático. Además, este modo nos impide disfrutar de las partidas, ya que realiza por nosotros los giros, que son parte del encanto y la emoción de jugar a las tragaperras. En todo caso podremos activar el juego automático en los giros gratuitos o en determinados premios extra, jugadas que no irán nunca en perjuicio de nuestro bankroll.

Tipos de slots

Antes de poner en práctica los consejos que acabamos de explicar, conviene conocer los distintos tipos de slots que nos podemos encontrar en un casino online: 

• Tragaperras con bote progresivo: sobre las slots con jackpot de casino podemos decir son tragaperras que cuentan con un bote acumulativo que aumenta conforme los sucesivos usuarios del juego van apostando, de modo que una pequeña porción de sus apuestas va a parar al premio común. Cuantos más jugadores haya y más apuestas se realicen, mayor será el bote que, finalmente, un sólo jugador se llevará.

• Video-slots: en la video slot se eliminan  los elementos propiamente mecánicos de las tragaperras clásicas y estos son sustituidos por animaciones y gráficos de última generación donde la interactividad con el usuarios se multiplica. El resultado es una slot ágil, divertida, detallista y, en ocasiones –como ocurre con las tragaperras 3D–, con una sección visual a la altura de los mejores videojuegos de Instant Gaming. Los minijuegos extra y la banda sonora ayudan a la experiencia inmersiva propia de estas slots.

Fuente: Youtube

• Tragaperras multiplicadoras: las slots cuentan con diferentes niveles de apuestas, y estas multiplican los premios otorgados según vamos aumentando el valor de dichas apuestas. 

Por otro lado, podemos clasificar las tragaperras según diferentes parámetros: 

• Líneas de pago: cada slot ofrece una cantidad de líneas de pago distinta. A veces estas son variables y otras fijas; en las primeras, serán los jugadores quienes elijan con cuántas líneas de pago de las ofrecidas desean jugar. Las tragaperras antiguas o las slots online de corte clásico disponen de entre 3 y 5 líneas de pago. Las más modernas pueden llegar a tener 20 o más. El caso más extremo lo encontramos en las tragaperras Megaways, que cuentan con una media de 100.000 líneas distintas de pago, una cifra mareante que posibilita una mayor probabilidad de ganancias. 

• Rodillos: ya sean mecánicos o digitales, los rodillos son aquellos elementos de la slot donde se ubican los símbolos. Estos rodillos girarán hasta formar combinaciones, tal vez ganadoras, de símbolos. Algunas slots, las más clásicas, disponen de 3 a 5 rodillos; las más modernas cuentan con 10. Lo más habitual, en todo caso, es encontrarnos con tragaperras de 6 rodillos. 

Aviso: Todos los consejos dados en este artículo tienen un carácter meramente informativo basado en bibliografía sobre juegos de azar. Sin embargo ninguno de estos consejos garantiza ni es un elemento determinante para el éxito en la actividad del juego analizado. En nuestro blog tratamos temáticas relacionadas con el mundo de los juegos y los contenidos son informativos y no significa que tengamos disponible el juego, producto, utensilio, accesorio, etcétera…del que habla el artículo.

• La ruleta electrónica es una modalidad de ruleta sin crupier en la cual la bola es lanzada automáticamente a través de un sistema de aire comprimido (si hablamos de ruletas físicas), o bien mediante software (si hablamos de ruletas online). 
• Las ruletas electrónicas aseguran la completa aleatoriedad de los resultados.
• Aunque existen ciertas teorías al respecto, lo cierto es que es imposible determinar de antemano qué números saldrán en la ruleta electrónica. 

 

Contenido:

• Qué es una ruleta electrónica
• Tipos de ruleta electrónica
• ¿Cuántos números tiene la ruleta?
• Entonces, ¿qué números salen más en la ruleta?
• Probabilidades de apuesta en la ruleta
• Números calientes y números fríos en la ruleta
• Ventajas de la ruleta electrónica
• Una cuestión de confianza
• Cammeh: la ruleta transparente
• ¿Quién fabrica estas ruletas electrónicas?
• ¿Cómo funcionan estas ruletas electrónicas?
• Sobre el mecanismo de la ruleta airball

Lejos de suponer un declive para los casinos, la revolución tecnológica de las últimas décadas ha significado un verdadero empujón de popularidad para clásicos como el blackjack o la propia ruleta. Los usuarios tienen la oportunidad de elegir entre jugar en los casinos presenciales o en el casino on line, donde se encontrarán un enorme catálogo de juegos de casino con ciertas comodidades y prestaciones inimaginables hace algunos años. Entre ellos destacan las ruletas electrónicas, protagonistas de nuestro artículo de hoy.  

Antes que nada, debemos tener claro qué es una ruleta electrónica: una ruleta electrónica es una modalidad de ruleta en la cual la bola será lanzada mecánicamente, sin mediación alguna de crupier o asistente que guíe en la partida. 

El mecanismo de la ruleta aleatoria funciona de manera completamente aleatoria y automática; la imparcialidad del juego es total, con lo que será imposible predecir o programar dónde caerá la bola. Como ocurre en otros juegos como las tragaperras online o el video poker, el azar manda. 

Diferenciamos, fundamentalmente, entre dos tipos de ruleta electrónica: 

Ruleta electrónica en casino presencial 

Se trata de las ruletas electrónicas automáticas que encontramos en los casinos físicos; estas se diferencian de las ruletas convencionales, entre otras cosas, en que no disponen de crupier que lance la bola y asista a los jugadores durante la partida; todo está automatizado. Descartamos pues cualquier ruleta streaming de casino en vivo puesto que, como sabemos, una de las características de esta modalidad es la asistencia permanente de un crupier. 

Estas ruletas electrónicas disponen de un mecanismo de aire que, controlado por el jugador, impulsará la bola con mayor o menor fuerza, dependiendo de su intención. 

Frame - Fuente: Youtube

Ruleta electrónica de casino online

En este caso nos referimos a las ruletas electrónicas online que podemos encontrar en 888casino o en cualquier casino móvil. Al registrarte puedes aprovechar un casino bonus, y en este tipo de ruletas la aleatoriedad de los resultados está absolutamente asegurada gracias a lo que se conoce como GNA; el generador de números aleatorio.

Los generadores de números aleatorios son un tipo de software que se integra en el juego de azar (en este caso la ruleta electrónica) para asegurar la completa imparcialidad de los resultados.  

Antes de ir al meollo del asunto, tenemos que conocer algo fundamental: cuántos números tiene una ruleta. Bien, vamos a verlo. Para empezar aclararemos que esto va a depender del tipo de ruleta. Si hablamos de la ruleta europea o ruleta francesa, comprobaremos que tiene 37 números (18 negros y 18 rojos) y un cero (de color verde). Por otro tenemos la ruleta americana; esta tiene 38 números (18 negros y 18 rojos) y al 0 le sumamos una nueva casilla verde de doble cero (00). 

La disposición de estos números de la ruleta de casino dependerá también de la versión a la que estemos jugando: los números de la ruleta europea (o francesa) están dispuestos aleatoriamente, en cambio en la ruleta americana siguen un orden lógico. En esta última, las casillas del 0 y el 00 estarán enfrentadas (de la misma manera que el 1/2 o el 3/4…). Tanto en la ruleta europea como en el americana veremos un número negro entre dos rojos. En la ruleta americana cada número par estará enfrentado siempre a uno impar. 

Por muchas teorías (y algunas supersticiones) que haya al respecto, lo verdad es que no puede conocerse de antemano qué números saldrán en la ruleta. La única certeza que tenemos en el juego de la ruleta es que solo el azar dictamina el resultado final. Lo lamentamos: no hay manera segura de saber cómo ganar en el casino. 

Otra cosa distinta es el estudio de las probabilidades en la ruleta (sabemos que en la ruleta francesa, por ejemplo, cada número tiene 1 posibilidad entre 37 de salir). También es muy útil la aplicación de ciertas estrategias de ruleta que favorecen al jugador frente a la banca, aumentando sus opciones de ganar (aunque hablamos de juegos donde el factor suerte es predominante, algunos juegos como el black jack online o la propia ruleta, admiten cierta planificación estratégica). 

Algunos casinos online facilitan cierta información de la ruleta, como por ejemplo los últimos números que han salido en más ocasiones, algo que puede ser útil (aunque no crucial). Pero recordemos; saber esto no nos resuelve nada, estamos jugando a un juego de azar y, como el propio nombre indica, solo la suerte dirá si ganamos o perdemos. 

A pesar de que existen leves diferencias entre los distintos tipos de ruletas, es muy conveniente conocer las mejores apuestas de ruleta que se pueden hacer y las probabilidades de cada una de ellas: 

En el contexto del juego de la ruleta de casino se conoce como números calientes a aquellos números que han salido en más ocasiones durante los últimos 500 giros o bien durante las últimas 24 horas. Por su parte, con el nombre de números fríos nos referimos a los que han salido menos veces en ese mismo periodo de tiempo o en esa misma cantidad de giros.

Esto no quiere decir que esos números calientes vayan a seguir saliendo con frecuencia, es tan sólo una foto fija en un momento dado. Como hemos dicho anteriormente, la realidad es que no puede predecirse qué números aparecerán; no hay garantía alguna de que apostar a los números calientes o fríos vayan a seguir siéndolo en los próximos giros y horas. 

Fuente: Youtube

• Las partidas de ruleta electrónica son más dinámicas y ágiles. El ritmo de juego lo marca el propio jugador y la automatización de la ruleta (sin la intervención del crupier) acorta los tiempos muertos. 
• No hay limitación horaria. Este tipo de ruletas de casino online permite una flexibilización respecto al tiempo y lugar que no se da en las ruletas convencionales: se jugará dónde, cómo y cuándo quiera el jugador.  
• El jugador no compartirá espacio con otros participantes, algo que, en muchas ocasiones, genera un alivio de la presión por competitividad. 
• El jugador dispone de información detallada y al instante del estado de la partida; esto puede darle una mayor perspectiva y sensación de control. 

La realidad es que tanto los casinos online como los presenciales cuentan con enormes medidas de control y sus productos están al alcance de cualquier aficionado que quiera estudiarlos y analizarlos. 

Pero para evitar suspicacias, los desarrolladores y fabricantes de ruleta trabajan para mejorar la transparencia del juego y producir innovadoras ruletas. Un buen ejemplo de ello es la ruleta de la que hablaremos a continuación; una ruleta está hecha con una rueda de vidrio con la finalidad de que el jugador pueda ver "dentro" y confiar plenamente en el juego.

Como decíamos, se trata de una rueda transparente de vidrio. Un dispositivo que nace como una forma de combatir ciertas suspicacias de ciertos jugadores frente a determinadas ruletas electrónicas conocidas con el nombre ruletas airball o fast roulette. 

Por lo general, los fabricantes de la industria del juego —particularmente en el juego online— están haciendo un gran esfuerzo de transparencia y pretenden arrojar luz sobre sus productos. Además de esto, hay que decir que todos estos juegos de azar están sujetos a la ley y debidamente regulados por instituciones gubernamentales como la Dirección General de Ordenación de Juego (DGOJ).

Los sistemas de ruleta europea airball o de dispositivo de aire comprimido, a menudo producidos en países de Europa del este, llegaron a los salones y casinos de juego a finales de los noventa. Las marcas más conocidas de la industria son Interblock, Elektroncek, Alfastreet, Gold Club, Spintec y los dos gigantes de la fabricación de juegos de casino y slots como Igt y Novomatic.

Otros modelos populares de ruleta electrónica son. 

• Ruleta electrónica Gold Club
• Modelo Cammegh Slingshot 2
• El RSS de Mercury 360

Para aquellos que no están familiarizados con el juego: la configuración generalmente de estas ruletas aleatorias consiste en una rueda eléctrica con rotor eléctrico cubierta por una cúpula de vidrio. La pelota se lanza al ser expulsada del bolsillo por una bocanada de aire. Varias consolas de jugadores se colocan estratégicamente alrededor del volante y los apostadores hacen sus apuestas usando pantallas táctiles hasta que se diga "no más apuestas".

Todas las ganancias o pérdidas se calculan electrónicamente. El intervalo de giros independientes generalmente se establece entre 60 y 90 segundos, asegurando un flujo de juego constante. El juego automatizado se vincula con el sistema de monitoreo central del casino para que el estado grave con precisión las ganancias.

En las ruletas electrónicas  "de aire comprimido" —a veces llamadas “ruletas rápidas”— la bola lanzada se mueve muy rápido; a más de 17 números por segundo. Después de que el crupier dice "no va más", hay otras 10 rotaciones mientras la velocidad de dicha bola y la rueda se desaceleran hasta la caída final. 

Es importante saber que las máquinas de air-ball, incluso del mismo modelo y fabricante, podrían tener diferentes configuraciones de juego y versiones de software, por lo que los valores presentados aquí no son representativos de todos los modelos de ruleta electrónica. Los consejos sobre como ganar en la ruleta electrónica, sin embargo, sí son válidos en general. 

 

Aviso: Todos los consejos dados en este artículo tienen un carácter meramente informativo basado en bibliografía sobre juegos de azar. Sin embargo ninguno de estos consejos garantiza ni es un elemento determinante para el éxito en la actividad del juego analizado. En nuestro blog tratamos temáticas relacionadas con el mundo de los juegos y los contenidos son informativos y no significa que tengamos disponible el juego, producto, utensilio, accesorio, etcétera…del que habla el artículo.

 

• En la ruleta americana, la ventaja de la casa es del 5,26%, mientras que en la ruleta europea dicha ventaja es del 2,70%
• Existen muchos tipos de apuestas de ruleta que conviene conocer a fondo si queremos tener opciones de ganar; desde las apuestas a números simples hasta las apuestas a columna
• Cada lanzamiento de ruleta es aleatorio e impredecible: el resultado no dependerá nunca de los anteriores lanzamientos

Contenido: 

• La importancia de los números
• Sobre los números de la ruleta
• Apostar a números simples
• Apostar entre dos números
• Las Apuestas Internas
• Apuestas a Docenas
• Apuestas a Columna
• Apuestas a pasa / falta
• Apuestas a rojo / negro
• Apuestas a par / impar
• Apostar al 0 en la ruleta
• Dos conceptos: Rendirse y En Prisión
• El peligro de las rachas

Sabemos que la ruleta es uno de los pasatiempos más demandados en cualquier casino online de España. Sabemos también que es un juego cuyos resultados dependen, fundamentalmente, de la suerte. Sin embargo, en las ruletas –a diferencia de lo que ocurre en otros juegos de azar– tiene cabida la estrategia: se trata de números, ceros, números altos, números bajos, números rojos, números negros, números impares, números pares y docenas de números. Hay números y combinaciones de números que hacen que los corazones de los jugadores de ruleta tiemblen de nervios y emoción. ¿Saldrán mis números? ¿O mis números me van a fallar? En este artículo te vamos a contar cómo jugar en la ruleta en una guía muy completa.

Tal vez el número que más deseamos es el que responde a la siguiente pregunta: ¿Cuánto dinero puedo ganar? Las ganancias también constituyen números. 

La ruleta es un juego antiguo, probablemente su origen lo encontramos en el siglo XVI, pero tal vez se remonte incluso más allá; se dice que los soldados romanos jugaban haciendo girar sus escudos…

¿Por qué los jugadores de juegos del casino están tan obsesionados con los juegos compuestos de números? Quizá porque, en realidad, siempre usamos números para descubrir dónde y cómo caminamos, corremos, nadamos, navegamos, conducimos un automóvil… Por supuesto, también los usamos cuando jugamos a juegos de cartas como black jack online, o cuando pasamos la tarde jugando a juegos tradicionales como el mahjong o el ajedrez.  

Es posible que no sepamos que todas estas actividades se reducen al uso de números, pero ciertamente lo hacen. Todos somos matemáticos, lo sepamos o no.

Entonces, ¿cómo debemos jugar los números de la ruleta? ¿Cuáles son las apuestas en la ruleta seguras? En primer lugar, debemos recordar que el juego tiene una ventaja para la casa. En la rueda estadounidense de doble cero, la ventaja es del 5,26 %. En la rueda europea de un solo cero, la ventaja es del 2,7 %. La ruleta americana tiene 38 números; La rueda europea tiene 37 números. El pago por un solo número interno es de 35 a 1 en ambas ruedas. Veamos pues cómo apostar a la ruleta…

Colocaremos nuestras fichas directamente en el tablero de la ruleta en un número o números individuales. El pago es de 35 a 1 y mantiene la apuesta inicial, lo que significa un 36 a 1.

• Pros: debido a que el pago es de 35 a 1 y una ganancia hace que eso sea muy beneficioso, muchos jugadores prefieren este estilo de apuestas. Si tienes la suerte de hacer un pleno pronto la ganancia siempre será muy grande.
• Contras: el patrón de victorias y derrotas es similar al de las máquinas tragamonedas, aunque peor, ya que solo tienes una probabilidad de 1 entre 37 o de 1 entre 38 para obtener un pleno, o lo que es lo mismo, acertar un número. Puede experimentar largos períodos de rachas perdedoras. Eso no es muy divertido y es muy poco productivo. Las slots en realidad pagan con más frecuencia, aunque su porcentaje de ventaja es generalmente mayor que el de la ruleta aleatoria, por mucho que sepas cómo jugar a la ruleta y ganar.

Coloca tu ficha en la línea entre dos números. Si alguno de los dos gana, ganarás 17 a 1 la cantidad apostada. Independientemente del tipo de ruleta. Incluso en las ruletas electrónicas no hay diferencias en pagos.

• Pros: con una apuesta puedes cubrir dos números aumentando tus posibilidades de ganar pero sin aumentar o disminuir la ventaja de la casa. Esto se aplica a todas las apuestas combinadas internas. A más números cubiertos por una sola apuesta, más posibilidades de victoria en ese giro. Aunque, obviamente, si resultan ganadores, la ganancia será menor al ser menor la cantidad apostada.

• Contras: la ventaja de la casa no cambia en absoluto en esta apuesta, pero tus posibilidades de ganar aumentan. Nuevamente, el jugador puede tener largas rachas perdedoras al apostar en las divisiones. Y una advertencia: ten cuidado de que otros jugadores no empujen accidentalmente su apuesta a un solo número o a un número diferente a la apuesta que deseabas realizar.

La primera es la denominada "Apuesta a calle", que consta de tres números. Para hacerla, coloca tu apuesta en la línea exterior de los tres números que deseas ganar. El pago es de 11 a 1.

• Pros: una apuesta, tres números cubiertos. Sí, esto puede reducir las rachas perdedoras.
• Contras: al colocar tu apuesta en una línea externa puedes encontrar que otros jugadores empujan accidentalmente sus fichas fuera de dicha línea. Tenga en cuenta esto, ya que sucede a veces. Es posible que, para realizar tu apuesta, desees esperar a que otros jugadores hayan terminado las suyas.

La segunda es la "apuesta al cuadrado", válida para todos los tipos de ruleta. Esta es una apuesta de cuatro números. Deberemos colocar nuestra apuesta en el área central de cuatro casillas para que tenga dos casillas encima de la apuesta y dos casillas debajo de la apuesta. En resumen, las líneas se cruzan en el medio de la apuesta. El pago es de 8 a 1.

• Pros: apuesta fácil de realizar. Las rachas perdedoras continúan reduciéndose.
• Contras: el gran problema es que otra vez alguien mueva tus fichas de la apuesta, ya que muchos jugadores pueden apostar cualquiera de estos números directamente.

Tercero: podemos apostar también a 5 números. Esta apuesta de cinco números solo se encuentra en la rueda americana de doble cero y cubre los números 0, 00, 1, 2 y 3. Tiene la ventaja más alta de la casa: un 7.89 %. Es una absoluta pérdida de dinero.

Como cuarta apuesta de este estilo, encontramos la de los 6 números. Esta es una apuesta de seis números que se coloca en la línea exterior que divide tres números de tres números. El pago es de 5 a 1.

• Pros: de nuevo, con una sola apuesta puedes cubrir 6 números internos. La reducción en las rachas perdedoras es lo mejor para este estilo de apuestas internas.
• Contras: hay una tendencia por parte de algunos jugadores que apuestan a los 6 números: querer cubrir cada vez más números en el interior. Eso hace que cuando hay malas rachas las pérdidas puedan ser muy grandes.

Algunos jugadores quieren cubrir aún más números internos pero no haciendo apuestas individuales, alejándose de la estrategia de ruleta simple, por lo que pondrán 2 o más de las apuestas combinadas internas anteriormente comentadas. No verás esto muy a menudo, pero es algo a tener en cuenta ya que estas apuestas se pueden repartir bastante y los jugadores no quieren que sus apuestas se salgan de esa área.

Encontrarás todas las apuestas externas que se pueden realizar en las partes externas de la mesa de la ruleta. Todas ellas te dan una mayor posibilidad de ganar que cualquiera de las apuestas internas anteriores. Algunos tienen casi 50-50, como en 18 victorias y 20 derrotas en la rueda americana y 18 victorias y 19 derrotas en la rueda francesa o europea. Los otros tienen hasta una docena de números y usted puede, si lo desea, apostar hasta 24 números apostando 2 de estas apuestas.

Si observas el diseño de la mesa de apuestas, comprobarás que los números del 1 al 12, del 13 al 24 y del 25 al 36 forman un conjunto. Estos conjuntos se llaman la primera docena, la segunda docena y la tercera docena. Hay un área de apuestas debajo de cada una de estas docenas para que un jugador haga sus apuestas. El pago de la apuesta "a docenas" es de 2 a 1. El cero o los ceros no cuentan como parte de las apuestas "docenas".

• Pros: apostar una docena de números con una apuesta generalmente reduce la fluctuación y largas rachas perdedoras experimentadas con las apuestas internas. Si apuestas dos de las docenas, obtienes 24 números de 37 y 38 números en los juegos respectivos.
• Contras: darte tantos números al principio puede parecer genial, pero ten en cuenta que cuanto más apuestes, ganarás más a menudo en estas apuestas pero también perderás más dinero con el tiempo, si no eres muy afortunado.

Hay otro tipo de "docena de apuesta" ubicada en una línea longitudinal en el diseño de la mesa de apuestas. Esta apuesta se llama apuesta de columna y va del 1 al 34; 2 a 35 y 3 a 36.

Estos números de la ruleta no están en orden numérico. La apuesta se realiza en la parte inferior de la columna y el pago de una apuesta ganadora es de 2 a 1. El cero o los ceros no cuentan como parte de las apuestas de columna.

Las ventajas y desventajas de las apuestas de columnas son las mismas que para las apuestas docenas anteriores.

Puedes apostar los números altos que van del 19 al 36 o los números bajos que van del 1 al 18. El cero o los ceros no cuentan como altos o bajos. El pago es 1 a 1.

• Pros: tienes 18 oportunidades de ganar y 20 oportunidades de perder en la rueda de doble cero (ruleta americana) y 18 oportunidades de ganar y 19 oportunidades de perder en la rueda de un cero (ruleta europea o francesa). 
• Contras: la ventaja de la casa no cambia.

Con la excepción del cero verde (s), los números en la ruleta son rojos o negros. Puedes apostar a cualquier color y el pago de una apuesta ganadora es 1 a 1. Los pros y los contras son los mismos que para las apuestas altas y bajas.

Nuevamente, con la excepción del cero verde (s), los números en la ruleta son pares o impares. El pago es 1 a 1.

Debes tener en cuenta que en la ruleta la apuesta inicial no es parte del pago, al contrario que en las tragaperras. Si una máquina paga 10 monedas en una línea, una o más de esas monedas serán la apuesta real. Cuando ganes una apuesta de ruleta, mantendrás la apuesta original y se te pagará el monto total. Por lo tanto, una victoria de 10 a 1 es en realidad 10 y se devuelve tu apuesta original.

Tipos de apuestas al 0 (ruleta francesa / ruleta europea)

El 0 forma parte de nuestras estrategias de ruleta y podemos apostar a él. Las apuestas plenas a 0 se pagan 36 a 1 pero existen otras opciones que conviene conocer: 

• Juego del cero: apostamos a 7 números próximos al 0 (incluyéndolo a este): 12, 35, 3, 26, 0, 32, 15. Este tipo de apuesta se paga 5 a 1. 
• Canasta: muy parecida a la apuesta al cuadrado pero aquí incluimos el 0. Cubrimos, de ese modo, la serie 0, 1, 2, 3. Esta apuesta se paga 9 a 1. 
• Vecinos del 0: apostamos a 17 números vecinos ruleta del 0 (incluyendo este). Usando 2 fichas cubriremos 0, 2, 3 y 25, 26, 28, 29; con una ficha tendremos 4-7, 12-15, 18-21, 19-22 y 32-35. Dependiendo de dónde caiga la bola el premio variará.
• El 0 y sus vecinos: en la ruleta online de España esta apuesta es habitual. Consistirá en añadir a la apuesta anterior (Vecinos del 0) una ficha más y jugar así un pleno al 0. Jugaremos a 17 números con 10 fichas.
• Trío: apostamos a una serie de 3 números con una única ficha: 0, 1, 2 o bien 0, 2, 3. Esta apuesta se paga 9 a 1.

Tipos de apuestas al 00 (ruleta americana) 

• A pleno: es la más importante; cuando hablamos del 0 y 00, este tipo de apuestas se pagan 35 a 1. 
• Apuestas a 5: esta apuesta incumbe solo a la ruleta americana y cubrirá la secuencia 0, 00, 1, 2 y 3. Es una apuesta similar a la de los 4 números de la ruleta europea pero adaptada a la ruleta americana. Se paga 7 a 1.

Algunos casinos online y offline ofrecen a los jugadores de ruleta la oportunidad de reducir la ventaja de la casa a la mitad. En lugar de contrarrestar una ventaja de la casa del 5.26 % en la ruleta americana o de doble cero, o bien una ventaja de la casa del 2.70 % en la ruleta de cero simple o ruleta europea, hacen que el jugador se enfrente a una ventaja del 2.63 % o del 1.35%, respectivamente. 

En una ruleta que permita la rendición, el crupier recogerá solo la mitad de tu apuesta cuando salga el 0 o 00 cuando haya apuestas a suertes sencillas (rojo/negro, par/impar). Por lo tanto, la ventaja de la casa se reduce al 2,63 % en las ruedas de doble cero y al 1,35 % en las ruedas de cero simple.

Y como ya debes saber, la ventaja de la casa del 1.35 % es una de las más bajas del casino.

Una ruleta que permite la regla "En prisión" también reduce a la mitad la ventaja de la casa de aquellos que realizan apuestas externas. Esta regla de ruleta se encuentra solamente en algunos de los juegos de ruleta de un solo cero. Es simple: si sale el cero, la apuesta queda bloqueada hasta el próximo giro de la rueda. Ganarás o perderás en el siguiente giro; no puedes tocarla...

Uno: puedes apostar la misma cantidad por el mismo período de tiempo en estas apuestas externas con rendición o en prisión y reducir las pérdidas esperadas a la mitad. Dos: puedes duplicar tu apuesta pensando que las ganancias serán más cuando se caliente. Tres: puedes emplear un sistema de apuestas de ruleta de dinero par. Entonces, ¿cuál es la mejor apuesta ruleta? En mi opinión, ¡la primera es la mejor opción!

Ciertamente, los jugadores pueden caer en la trampa de pensar que las tendencias dominarán y serán predecibles. ¿El rojo ha salido seis veces? ¡Debe estar caliente! ¡No, no, está a punto de enfriarse! Pero ya sabemos que los lanzamientos de ruleta son sucesos aleatorios e independientes…

En esta tabla de arriba te damos una explicación visual para que comprendas las probabilidades que tiene cada jugada si juegas y apuestas ruleta americana.

Puedes estructurar tu "sistema" de apuestas como quieras pero tanto la ruleta online como la ruleta del casino en vivo son aleatorias y sus resultados, por lo tanto, impredecibles, sin importar lo que parezca a corto plazo.

Como hemos hecho antes con la americana, te mostramos ahora la tabla de pagos y probabilidades de la ruleta francesa o europea.

 

Aviso: Todos los consejos dados en este artículo tienen un carácter meramente informativo basado en bibliografía sobre juegos de azar. Sin embargo ninguno de estos consejos garantiza ni es un elemento determinante para el éxito en la actividad del juego analizado. En nuestro blog tratamos temáticas relacionadas con el mundo de los juegos y los contenidos son informativos y no significa que tengamos disponible el juego, producto, utensilio, accesorio, etcétera…del que habla el artículo.

Aviso: Todos los consejos dados en este artículo tienen un carácter meramente informativo basado en bibliografía sobre juegos de azar. Sin embargo ninguno de estos consejos garantiza ni es un elemento determinante para el éxito en la actividad del juego analizado. En nuestro blog tratamos temáticas relacionadas con el mundo de los juegos y los contenidos son informativos y no significa que tengamos disponible el juego, producto, utensilio, accesorio, etcétera…del que habla el artículo.

• Las tragaperras fueron y siguen siendo, en su versión online, uno de los juegos de azar de más éxito en España. 
• Existe una oferta inmensa de slots y una buena forma de clasificarlas es según su temática. 
• La tragaperras Gnomos Mix es de temática fantástica; está ambientada en un universo mágico poblado de hadas, gnomos, bosques encantados y tesoros por descubrir. 
• Detrás de Gnomos Mix está el veterano y prestigioso desarrollador español Recreativos Franco.

Contenido: 

• Retorno a las tragaperras clásicas
• 5 tipos de tragaperras según su temática
• Las tragaperras online y su regulación
• Tragaperras online en 888Casino
• El universo mágico de la tragaperras Gnomos Mix 
• Gnomos Mix: características
• Cómo se juega a Gnomos Mix
• Jugar gratis a Gnomos Mix

Las tragaperras son uno de los juegos de azar online más populares. De hecho, atendiendo a los datos que cada trimestre publica la Dirección General de Ordenación de Juego, el producto de Tragaperras o slot es el preferido por los clientes de los operadores de casino online en el mercado regulado español. Evidentemente, por tratarse de uno de los juegos de casino online más importantes, el número de juegos, las temáticas y la calidad de los mismos es fundamental. Además, con ánimo de respetar la tradición y las costumbres típicas de los jugadores españoles, la oferta de tragamonedas online en nuestro país cuenta con réplicas y títulos basados en las tragaperras españolas que tanto triunfaron en los bares y salones de los años 80 y 90.

En este artículo repasaremos algunas de las máquinas tragaperras más exitosas y las clasificaremos según su temática y atendiendo a otras características igualmente importantes. Haremos hincapié, sin embargo, en las de temática fantástica y de aventuras; en concreto en la slot Gnomos Mix. Esta tragaperras nos servirá como ejemplo para analizar toda una generación de tragamonedas que ha sabido actualizar y modernizar las slots de estilo clásico.  

Las tragaperras antiguas son cada vez más demandadas por los jugadores. Principalmente porque resulta atractivo poder disfrutar en internet de las sensaciones que hemos tenido años atrás cuando solamente se podía jugar a las tragaperras en un bar o en una cafetería.

Y es que si abordamos el tema de las máquinas tragaperras en España, debemos en primer lugar destacar que durante muchos años las slots se convirtieron en uno de los entretenimientos más populares y aceptados socialmente. Desde la legalización del juego a finales de la década de 1970, las máquinas tragaperras españolas podían instalarse sin problemas en bares y restaurantes de cualquier ciudad. Esto propició su masiva aceptación como una forma de entretenimiento habitual en la que invertir unas monedas tras realizar nuestra consumición. Pero al mismo tiempo, desde siempre, se han visto como uno de los mejores juegos para ganar dinero.

Por otro lado, las tragaperras son también un juego propio del casino y del salón de juegos, por lo que la legislación al respecto tuvo que diferenciar entre diferentes tipos de máquinas tragaperras atendiendo a los premios que otorgan y a los sistemas técnicos de las mismas. En resumidas cuentas, los establecimientos de restauración cuentan con máquinas tragaperras de menor precio y menor premio; mientras que cuanto mayores son los premios y el precio de las jugadas, las máquinas tragaperras se instalan en salones de juego o en alguno de los casi medio centenar de casinos de España.

Desde la llegada de esas tragaperras clásicas a casinos, salones, bares y restaurantes, los fabricantes de slots han iniciado una enorme carrera por crear las máquinas tragamonedas más atractivas para el jugador. Y esto se hace de dos formas: mejorando los premios o creando las mejores slots a nivel de tecnología y temáticas. Es en este segundo aspecto donde las tragaperras muestran una evolución más importante; se ha pasado de una temática fija como ocurría en los juegos de frutas de los años 70 y los 80 a otras mucho más variadas que incluyen ambientaciones espaciales, de terror, aventuras gráficas e incluso juegos de slots protagonizadas por personajes de ficción de series tan famosas como la tragaperras Narcos. 

Así pues, de la misma manera que se hace con las películas o las novelas, las tragaperras se pueden clasificar según su género o temática. Si tomamos como ejemplo las slots disponibles en 888 casino podríamos realizar una lista de 5 temáticas:

1. Las slots de aventuras: en esta categoría encontramos las slots de aventuras marinas como “Mermaid´s Millions” o todas las relacionadas con Piratas.

2. Las tragaperras sobre mundos fantásticos y mitológicos: entre los juegos más destacados tendríamos Gods of Gold, la tragaperras Magic Mirror, Gnomos Mix y todos los títulos que podemos encontrar sobre mitología griega o nórdica.

3. Slots sobre civilizaciones antiguas: las experiencias de juego que generan títulos como Voyage of The Vikings, Eye of Horus, Rise of the Pharaohs, Aztec Realm, Wild Saloon están relacionadas con momentos históricos o civilizaciones antiguas. Encontramos desde los cowboys hasta aventuras centradas en el mundo de las culturas precolombinas como Incas o Aztecas. 

Fuente: Youtube

4. Slots de acción: con temáticas más modernas y con ambientaciones propias de los videojuegos arcade. En 888 casino encontramos títulos como Mystic Mask, Once Upon a Dime, Book of Legends, Jack´s Pot, Knights and Maidens. 

5. Tragaperras de temática de terror: Noche de Los Muertos, Transylvania Manía o The Unholy son títulos que junto a otros protagonizados por personajes como Freddy, de Pesadilla en Elm Street, forman parte de los juegos que ofrecemos en nuestra sección de slots online.

Gracias al éxito de las slots o máquinas tragaperras en nuestro país, la Dirección General de Ordenación de Juego se vio obligada a ampliar la oferta de juegos regulados en el mercado de juego online en España. Y es que en 2012, el año en el que se legalizó el juego online, sólo se concedieron licencias para operar a los siguientes juegos de casino: ruleta, blackjack online  y Punto y Banca. Además de esos tres juegos, también se ofreció a los operadores de juego online contar con poker online, bingo y con apuestas deportivas. 

Fue en 2015 cuando decidió regular el juego de las slots online. Para asegurarse de que esta oferta de juego cumplía con el objetivo de ser responsable, se incluyeron algunas condiciones que obligan a cada jugador a limitar el tiempo de sus sesiones de juego y decidir de antemano cuánto dinero del saldo disponible se quiere invertir en dichas sesiones, algo que ayuda a cumplir uno de los consejos de slots más importante que podrás leer: el de controlar el tiempo que inviertes y centrarse en cada una de tus tiradas.

Una vez se cumple con estos requisitos previos en favor del juego integral y responsable, se puede seleccionar la slot favorita entre los cientos de modelos que, por ejemplo, tiene 888 casino, ya sea en su versión para ordenador o la versión de casino móvil que te permite jugar desde tu smartphone o tablet. 

Gracias a esta enorme oferta, que incluye las temáticas tradicionales que ya hemos comentado, cualquier jugador de 888 casino puede jugar gratis a máquinas tragamonedas de última generación creados por los desarrolladores internacionales más importantes (NetEnt y Playtech, entre otros) y proveedores como la propia 888, que se ha convertido en una de las compañías de juego con slots online más destacadas de Europa. Entre otros muchos, dispone de juegos de éxito como Greedy Dragon, Gods of Gold Mystics Mask, Happy Faces o The Unholy. 

En todo caso, de lo que puedes estar seguro es de que las slots online te sorprenderán por la experiencia de juego que son capaces de ofrecer gracias a unos gráficos espectaculares con animaciones en 3D y un enorme abanico de sonidos envolventes.

Cómo acceder a las slots online de 888casino

Para disfrutar de las slots y máquinas tragaperras de 888casino simplemente tienes que acudir a la sección “Slots y Botes” y seleccionar tu juego favorito. Tenemos 5 categorías en las que dividimos toda la oferta de slots disponibles: 

• Las que están conectadas por jackpot o bote de casino común (Bote) 
• Las creadas por el propio desarrollador de 888 (888 original)
• Las desarrolladas por otras prestigiosas compañías (NetEnt, Playtech..) 
• Las que cuentan de 1 a 25 Líneas y las que tienen más de 25 Líneas

En todos esos grupos encontrarás juegos clásicos, juegos de aventuras, juegos tradicionales de frutas, juegos ambientados en civilizaciones antiguas y juegos de fantasía como Gnomos Mix, tragaperras que analizaremos a continuación. 

La tragaperras Gnomos Mix está ambientada en un universo fantástico poblado por hadas, árboles encantados, setas rojas y flores. En este mundo mágico protagonizado por los gnomos (que eran, según algunas leyendas, los que extraían las gemas y piedras preciosas de la tierra) se esconden todo tipo de tesoros y monedas de oro que tendremos que ser capaces de obtener. 

Gnomos Mix es un juego desarrollado por la mítica Recreativos Franco, una compañía ya veterana con más de 250 títulos a sus espaldas, entre los que destacan la tragaperras Santa Fe o Confidential. Gnomos, una de las tragaperras españolas más exitosas, podría enmarcarse dentro de las calificadas como “clásicas”; dispone de 3 rodillos y toda una serie de símbolos conocidos como son las frutas, los diamantes o las campanas. Estos símbolos se combinan con otros diseñados ad hoc, acorde con la temática del juego, como son los de la abeja o el bosque encantado. 

Esta tragaperras hará las delicias de los aficionados a las slots tradicionales ya que, además de los mencionados 3 rodillos y los símbolos de frutas, la barra de mandos imita a los de aquellas máquinas que disfrutábamos en tantos bares de España. Esta tragaperras cuenta con las funciones de avance y scatter.   

Tenemos, por tanto, una slot que, como sucedía en otra de las celebradas creaciones de Recreativos Franco, Neópolis, combina un escenario fantástico y una mecánica de juego simple, de estructura ya conocida. Además (como pasaba también en Neápolis y en Rainbow Riches, otra tragaperras emparentada temáticamente con Gnomos), los gráficos tienden más al cómic que al realismo épico de slots modernas tipo El dorado. 

 

Fuente: Youtube

La tragaperras Gnomos Mix no dispone de juego automático y está dividida en dos zonas, la del juego inferior y la del juego superior, cada uno con sus propias particularidades:

Juego inferior

Este juego dispone de 3 rodillos y una línea de pago. No es, por tanto, el juego más difícil del mundo, pero sí resulta muy divertido y ameno. Tiene los clásicos símbolos (frutas, campanas y diamantes) de las tragaperras tradicionales de bar y dos símbolos especiales que pueden dar pie a un mini juego extra con su consecuente premio. 

Si el jugador logra una combinación ganadora alineando 3 símbolos del bosque encantado tendrá acceso al minijuego de “Los calderos”, pudiendo así ganar hasta 43 créditos. 

El símbolo de la abeja es característico de la slot Gnomos: si esta figura aparece 1 vez, el jugador obtiene 1 premio, si aparece 2 veces obtendrá 2 premios y si lo hace 3, serán 6 premios.  

La señal de Giro Extra (antes de que se detenga el rodillo) indica giros gratuitos. 

Juego superior

El juego superior tiene 8 líneas de pago y se accede a él acumulando una serie de premios. En este juego superior el jugador se va a encontrar con los símbolos (setas rojas, flores…) que pueden dar acceso a una serie de mini juegos: 

• Juego de las fresas: cada rodillo esconde un premio que el jugador tratará de conseguir.
• Juego del tesoro: el jugador deberá escoger la mayor cifra desvelando uno de los rodillos. 
• Juego de las 3 opciones: el jugador deberá elegir, para obtener el mejor de los premios, entre 3 posibilidades.
• Juego de las 9 posiciones: el jugador deberá elegir la cifras de premio en 9 posiciones (hasta que aparezca el “Stop”). 

Si el símbolo de la bolsa cargada de dinero aparece en algún momento del juego superior, el jugador obtendrá automáticamente 5 premios. 

Puedes jugar a la versión gratuita de Gnomos Mix en tu dispositivo móvil y de esa manera conocer la slot en profundidad antes de decidirte a jugar con dinero real. Al principio percibirás 10.000 en monedas ficticias; deberás entonces seleccionar una de las 3 apuestas que la slot te propone. Estas apuestas irán desde un mínimo de 0,20 créditos hasta un máximo de 1 crédito. Para un mayor rendimiento de la partida deberás hacer uso, en caso de obtener 2 símbolos idénticos, de las funciones de avance y retención. 

 

• La ruleta es el juego estrella de los casinos y, desde su invención en el siglo XVII, ha vivido una transformación asombrosa.
• De la ruleta francesa original surgieron la variante europea y la ruleta americana; más tarde, con la llegada de internet, aparecieron las ruletas en vivo y las ruletas virtuales de los casinos online. 
• Además de la ruletas mencionadas, existen ruletas online personalizables que no pertenecen al ámbito de los juegos de casino. 

Contenido: 

• La ruleta americana
• La ruleta francesa
• La ruleta europea
• La ruleta Relámpago
• La ruleta Quantum
• La ruleta Casiopea
• Simulador de ruleta
• Ruletas online personalizables

Si hay un juego que representa como ningún otro a los juegos del casino, ese es la ruleta. Asociamos el casino on line o el salón de juego presencial a la figura del crupier, a la ruleta de números rojos y negros girando y a la bola decantándose por una de las casillas. La ruleta online comparte pódium con las tragaperras online o el blackjack online, pero sólo ellas simbolizan el glamour legendario de los casinos de Las Vegas o Francia, inmortalizadas en numerosas películas y novelas.

Por otro lado, es uno de los juegos de azar más antiguos; su origen se remonta a la Francia del siglo XVII. A partir de ahí el juego de la ruleta ha ido evolucionando y transformándose en las distintas modalidades que hoy conocemos; la ruleta europea, la ruleta francesa actual y la ruleta americana. Pero también los distintos tipos de ruleta en vivo y online de última generación, las ruletas virtuales personalizables que ofrecen usos distintos a los propios de los casinos o la ruleta electrónica.  

De todas ellas vamos a hablar en el artículo de hoy. 

La ruleta americana dispone de 38 números: los comprendidos entre el 1 y el 36, rojos y negros alternativamente, y el 0 y 00 (doble cero) de color verde. 

El doble cero es una característica distintiva de este tipo de ruleta y está ubicado en la ruleta frente al cero simple. Por su parte, los números de color rojo estarán ubicados frente a los negros: el 1 frente al 2 y, siguiendo esta misma lógica, el resto de números. El cero simple estará rodeado de números negros y el doble cero de números rojos. 

Una de las apuestas más habituales en la ruleta americana es la conocida como “apuesta de los 5 números'', en referencia a la secuencia 0, 00, 1, 2 y 3. Dicha apuesta permite, con una única ficha, abarcar 5 números en la línea superior. El jugador saldrá ganador si alguno de los 5 números sale premiado. El pago será de 5:1.

La apuestas múltiples y la apuestas suertes sencillas se realizarán como en el resto de ruletas. En la ruleta americana, estas suertes sencillas (falt/pasa, rojo/negro y par/impar) se encuentran a un único lado de la mesa. Este lado lo ocuparán los jugadores; frente a ellos, el crupier. 

Un dato curioso: pese a lo que muchos aficionados creen, la ruleta americana es más fiel a la ruleta europea original del siglo XVII. Esta última disponía, como ocurre en la americana actual, del doble cero (00), elemento que sólo posteriormente, en los años 30 del siglo XIX, se eliminó. 

La ruleta francesa consta de 37 números: los 36 primeros alternados en casillas rojas y negras y 1 sólo 0 de color verde. 

En la mesa de la ruleta francesa vemos una cuadrícula externa con un espacio diseñado para realizar apuestas simples. Estas apuestas simples se refieren a los números comprendidos entre 1 y 18 (números bajos o menores), los que van del 19 al 36 (números altos o mayores). En la zona inferior del tapete está el espacio para las columnas, la docena (primero, medio y último). 

En la ruleta francesa existen, además, determinadas apuestas especiales pero esto depende de cada casino, de modo que es conveniente consultar con detenimiento las reglas del que hayamos elegido para jugar. Sin embargo, algunas reglas especiales son casi siempre comunes a todos ellos. Dos de ellas son la “prisión” y la “partage”, ambas caracterizadas por aumentar la ventaja del jugador. 

En prisión: si la bola se para en el cero y el jugador ha realizado una apuesta simple externa podrá elegir entre perder la mitad de su apuesta o bien poner “en prisión” dicha apuesta durante el siguiente turno de lanzamiento, esperando que este le sea favorable. 

La partage: si la bola se para en el cero y el jugador ha realizado una apuesta simple externa, el casino le devolverá la mitad de su apuesta.  

Un dato curioso: tanto la ruleta francesa como su tapete y mesa son más grandes que los de la ruleta americana. Debido a ello se necesitan más crupiers (hasta 3): de ahí el uso de los rastrillos para las fichas y la presencia de un encargado de la mesa.  

La ruleta europea tiene, exactamente como la ruleta francesa, 37 números: los comprendidos entre el 1 y el 36, a los que sumamos el 0 simple. La mesa y el tapete son, sin embargo, más parecidos a los de la ruleta americana, de menor tamaño que los de la ruleta francesa y con las apuestas escritas en inglés. 

En la ruleta europea, tanto las apuestas internas como las externas coinciden con las de las modalidades americana y francesa. En cambio, algunas apuestas propias de la ruleta francesa no las encontraremos aquí, como las apuestas en huérfanos o en serie. 

Observamos un espacio de juego en la mesa (comúnmente llamado “pista de carreras”) que emula la distribución de los números de la ruleta, lo que facilita la colocación de apuestas especiales (la ficha irá directamente sobre la zona deseada). 

Un dato curioso: esta modalidad es especialmente popular en algunos países de Europa como Italia y, como hemos visto, combina elementos de la ruleta americana y la ruleta francesa. La mesa, al ser algo más reducida, junto con la administración de un croupier y la ausencia de rastrillos para las fichas, hace que la dinámica d ejuego sea más rápida y fiable. 

La irrupción de internet en el ámbito del gambling supuso una verdadera revolución de la cual surgieron novedosas versiones de los clásicos juegos de casino. Juegos con cartas inglesas o baraja francesa como el blackjack o el poker se convirtieron en el blackjack online y el video poker; las tragamonedas con dinero real se transformaron en slots virtuales; las ruletas se modificación con modernas prestaciones dando lugar a la ruleta Casiopea, la ruleta Quantum o la ruleta Relámpago. 

La ruleta Relámpago es una actualización y renovación de la clásica ruleta europea de casino. Se trata de una ruleta en vivo desarrollada por la compañía Evolution y ofrece interesantes mejoras con respecto a las ruletas convencionales. Una de estas mejoras tiene que ver con el notable aumento de la ventaja de los jugadores con respecto a la banca. Las probabilidades de ganancia crecen a razón de 499:1. 

La mecánica de juego de la ruleta tradicional se mantiene pero la ruleta relámpago añade distintos multiplicadores y sus “Números de la suerte” (lucky numbers): una vez se hayan hecho las apuestas, el crupier (no olvidemos que estamos ante una ruleta en vivo, por lo que contará con crupiers reales) pondrá en marcha el generador de números aleatorios que elegirá hasta 5 números de la suerte que pueden multiplicar la apuesta hasta x500 veces, lo que supone un premio realmente alto e inusual. 

A diferencia de las ruleta tradicionales de casino y un nuevo aliciente para los jugadores más intrépidos es que la dinámica del juego es mucho más emocionante y rápida ya que la ruleta gira a mayor velocidad. En este sentido, la ruleta relámpago tiene la misma velocidad de vértigo que la ruleta electrónica y para ganar en la ruleta electrónica hay que pensar mucho más rápido.

En este punto, debemos siempre recordar al lector que, por mucho que algunos juegos ofrezcan la posibilidad de grandes recompensas, estas siempre van a depender del azar. Es cierto que, a diferencia de lo que ocurre en otros juegos de casino, en las ruletas podemos aplicar estrategias de ruleta que pueden hacer aumentar nuestra ventaja, algo que no ocurre en, por ejemplo, las slots, aunque haya trucos para las tragamonedas de los bares o se conozcan las 10 trampas en slots que cambiaron la industria.  

Sí, las ruletas forman parte de los 6 juegos a los que puedes ganar en el casino, pero hay que jugar siempre con cabeza y con prudencia. 

Frame - Fuente: Youtube

Otras de las ruletas en vivo más interesantes que puedes encontrar en los casinos online es la ruleta Quantum de Playtech. 

Con una RTP del 97’30% deducimos que se trata de una ruleta con grandes ventajas para el jugador medio de ruleta. Sin embargo, las apuestas directas se pagan a razón de 29:1, un porcentaje algo bajo con respecto a la ruleta europea clásica. Una deficiencia que se ve compensada en parte por la calidad de sus multiplicadores, que pueden llevarnos a ganar premios bastante más altos que los ofrecidos por la ruleta europea: hasta x500 veces la apuesta.

Cada vez que la bola gire, el software elegirá de manera aleatoria al menos 2 de estos multiplicadores, que funcionarán únicamente con las apuestas directas. 

La ruleta casiopea permite también hacer apuestas sencillas. 

Por lo demás, la ruleta casiopea tiene un mecanismo de juego similar al de la ruleta europea. 

Fuente: Youtube

Tal y como ocurre con la ruleta Quantum y con la ruleta Relámpago, estamos ante una ruleta en vivo. Y como aquellas, guarda numerosas características en común con la ruleta europea clásica: un único cero y 36 números que se alternarán en casillas rojas y negras. De igual manera, las apuestas sencillas se encontrarán a los dos lados del tapete.   

En la ruleta Casiopea, los  jugadores pueden apostar desde un mínimo de 0,50€ hasta un máximo de 25.000€, un radio mucho más amplio que el que existe en otros tipos de ruleta. 

En la ruleta Casiopea los jugadores podrán activar un chat en vivo en el que poder consultar con el crupier el estado de la partida y cualquier duda sobre el juego que tenga. 

El simulador de ruleta es una herramienta online que reproduce todas las funciones de una ruleta de casino. La diferencia es que en estos simuladores no se apuesta con dinero real, por lo que los jugadores podrán aplicar sus estrategias y familiarizarse con el juego con absoluta tranquilidad, ya que no está en riesgo su economía. Son, por tanto, herramientas muy útiles antes de lanzarse a apostar en el casino online o en los salones físicos. 

Además del aliciente de su gratuidad, no sentiremos tampoco la presión del tiempo, ya que no existe esa fastidiosa cuenta atrás para colocar las apuestas antes del “no va más” del crupier. Por tornado, estos simuladores suelen ofrecer información muy útil para nuestro juego como, por ejemplo, una estadística detallada de los últimos números cubiertos con las apuestas realizadas.  

Existen simuladores de todo tipo de ruleta: americana, europea, francesa y otras…

Fuente: Youtube

Más allá de las ruletas de casino y de sus simuladores, existe otro tipo de ruleta online personalizable que puede servir a multitud de objetivos. La mayoría de estas ruletas aleatorias se usan para introducir un elemento de aleatoriedad en una determinada toma de decisiones. Por ejemplo, si queremos realizar un sorteo, un concurso o simplemente elegir al azar a una persona en un determinado evento sin levantar la más mínima sospecha de parcialidad. Un uso muy habitual de este tipo de ruleta aleatoria es el que se hace en ciertas clases, proceso que se conoce como “gamificación” de la aulas: mediantes estas ruletas virtuales introducimos el juego en el aprendizaje, dinamizándolo y en definitiva, haciéndolo más divertido. 

Dos de las ruletas aleatorias más populares, ambas gratuitas y que podemos encontrar con facilidad en internet, con la de la web Piliapp, y la Fluky ruleta.  

Fuente: Youtube

 

Aviso: Todos los consejos dados en este artículo tienen un carácter meramente informativo basado en bibliografía sobre juegos de azar. Sin embargo ninguno de estos consejos garantiza ni es un elemento determinante para el éxito en la actividad del juego analizado. En nuestro blog tratamos temáticas relacionadas con el mundo de los juegos y los contenidos son informativos y no significa que tengamos disponible el juego, producto, utensilio, accesorio, etcétera…del que habla el artículo.

 

• Ultimate Texas Hold’em es una variante del póker que se juega solo contra el crupier
• Se reparten siete cartas y hay tres rondas en las que puedes decidir si apostar o no
• Bien jugado, puede ofrecer una ventaja para el jugador similar a la del blackjack

 

Aunque en nuestro blog de juegos de casino online no solemos centrarnos en el póker, vamos a hacer una excepción. Modalidades como Casino Hold’em o Three Card Poker han ganado mucha popularidad y en este artículo hablaremos de una de las variantes más conocidas: el Ultimate Texas Hold’em. Se trata de una versión simplificada del clásico Texas Hold’em, pensada para jugar contra la banca en lugar de contra otros jugadores.

Nuestro experto en juegos de casino, John Grochowski, ha preparado una lista con 10 cosas que deberías saber antes de jugar a Ultimate Texas Hold'em. No se trata de un manual ni una guía de estrategia avanzada, pero sí de una introducción sencilla y útil, ideal para quienes quieran entender cómo ganar en el casino con este juego. 

A continuación, 10 consejos para que juegues lo mejor posible al Ultimate Texas Hold’em.

10 consejos para jugar al Ultimate Texas Hold'em

1. En Ultimate Texas Hold’em juegas contra el croupier

No tienes que intentar evaluar las manos de otros jugadores, ni hay ningún farol como pasa en el póker Texas Hold’em o en el Omaha. En Ultimate Texas Hold’Em, para ganar, tu mano debe vencer a la del crupier. Y es más que suficiente. Las manos de otros jugadores no te importan.

2 - No hay comisión directa como en el póker online.

En el poker de casino, ya sea jugando a Texas Hold’em, Omaha o Seven Card Stud, la casa gana dinero quedándose con un porcentaje del bote de cada mano.

En Ultimate Texas Hold’em no funciona así. En este juego de azar, la casa tiene cierta ventaja, por lo que no hay comisiones explícitas ni por mano ni por tiempo.

3 –La habilidad importa en Ultimate Texas Hold’em

Poco importa la habilidad si estás jugando a las slots. Sin embargo, los aficionados a la ruleta (no importa si es la clásica ruleta francesa o la moderna Mega Fire Blaze Roulette), el blackjack o poker saben bien que un conocimiento profundo del juego y la aplicación de ciertas estrategias puede marcar la diferencia. 

En el contexto de una partida de Ultimate Texas Hold’em: si sabes cuándo mantener la apuesta y cuándo doblarla, la ventaja de la casa se reduce a un 2,2 % sobre la apuesta inicial, o alrededor de un 0,5 % del total apostado. No es una ventaja muy alta si juegas bien, pero como ocurre cuando cometemos errores en los dados, una mala decisión puede salir muy cara.

Por cada 100 € apostados, la pérdida media teórica es de 2,20 €, una cifra baja en comparación con otros juegos de mesa. Esto significa que tienes opciones reales de ganar si tomas buenas decisiones y encadenas una buena racha.

Sin embargo, los jugadores que no aprenden estrategias básicas y son demasiado agresivos en sus apuestas se enfrentan a mayores ventajas del live casino o del casino online.

4 – Se reparten siete cartas, pero solo cuentan las mejores cinco

Tanto los jugadores como el crupier reciben dos cartas boca abajo. Son cartas propias y solo se usan para formar tu mano.

Las otras cinco cartas son comunitarias y pueden usarse por ambos, jugador y crupier. Se reparten en dos fases: primero tres cartas (el flop) y después dos más (turn y river). De las siete cartas en total, se elige la mejor combinación de cinco para formar la mano final.

5 - Todos los jugadores de Ultimate Texas Hold’em deben hacer apuestas ante y apuestas ciegas.

En Ultimate Texas Hold’em, ambas apuestas deben ser iguales: si el ante es de 5 €, también debemos apostar 5 € en la ciega.

El ante te permite jugar contra el crupier, y la ciega da acceso a pagos más altos si consigues una buena mano.

6 - Hay tres rondas de apuestas

Tras recibir tus dos primeras cartas, puedes apostar hasta cuatro veces tu apuesta inicial.

Si decides esperar, tendrás una segunda oportunidad después de que se repartan las tres primeras cartas comunitarias. En ese momento, puedes añadir una apuesta del doble de tu apuesta inicial, como sucede en algunas jugadas de blackjack.

La última ronda llega tras las dos cartas comunitarias finales. Si aún no has apostado, puedes hacerlo ahora con una cantidad igual a tu apuesta inicial.

Cuanto antes apuestes, más puedes apostar… Y más puedes ganar si tus cartas son buenas.

7 - No necesitas apostar hasta ver todas las cartas

En las partidas de poker, si no igualas la apuesta de otros jugadores, te retiras.

En Ultimate Texas Hold’em no funciona así. Si no apuestas tras recibir tus dos cartas o tras el primer grupo de cartas comunitarias, puedes seguir en la partida hasta la última ronda.

Una vez repartidas todas las cartas comunitarias, sí tendrás que tomar una decisión final: hacer tu apuesta o retirarte. Pero al menos habrás visto todas las cartas antes de decidir.

8 - El crupier necesita una mano mínima para abrir el juego

Para que el crupier pueda ‘abrir’, debe tener al menos una pareja. Tu apuesta principal se juega igual, pero si el crupier no abre, te devuelven la apuesta inicial y la ciega se paga según la tabla.

Veamos dos ejemplos:

• Haces una apuesta inicial de 5 € y otra adicional de 5 €. Tu mano es Rey alto y el crupier tiene Dama alta. Como no tiene pareja, no abre. Resultado: ganas la apuesta adicional y se te devuelve la inicial.
• Ahora imagina que tú tienes Rey alto y el crupier As alto. Tampoco abre, pero te gana. En ese caso, pierdes la apuesta extra, pero la inicial se devuelve igualmente.

9 - Puedes llegar a ganar 500 veces en valor de tu apuesta.

Las apuestas a ciegas se pagan de acuerdo con una tabla de pagos, independientemente de si el crupier abre. En esta tabla, están las manos ganadoras y los pagos.

10 - Las apuestas secundarias tienen sus propios pagos

Trips es una apuesta paralela opcional: no es obligatoria y solo se paga si logras un trío o mejor.

No importa si juegas en un casino online o en un casino móvil: las tablas de pago no cambian. El pago mínimo es de 3 a 1 por cualquier trío y alcanza un máximo de 50-1 en una escalera real. También hay pagos por color y poker, como podemos ver en la tabla.

Aunque todos los pagos comienzan en 3 a 1, el objetivo de esta apuesta es recompensar manos poco comunes. La probabilidad de obtener una mano ganadora ronda una de cada 6,5, mientras que el premio máximo de 50 a 1 ocurre en torno a una vez cada 30.000 manos.

Como sucede con 21+3 blackjack, estas apuestas paralelas suelen tener una ventaja más alta para el casino. La tabla de blackjack muestra claramente que estas jugadas extra rara vez compensan a largo plazo, por lo que conviene considerarlas solo como una opción puntual. 

Ultimate Texas Hold'em: preguntas y respuestas

¿Se puede jugar a Ultimate Texas Hold’em en España?
No. Este nombre de juego de casino aún no ha sido aprobado por la DGOJ, así que no está disponible en los casinos online legales en España.

¿Contra quién se juega en Ultimate Texas Hold’em?
No compites contra otros jugadores, solo contra el crupier, como en varios juegos de casino en vivo.

¿Cuántas cartas se reparten en Ultimate Texas Hold’em?
En total se reparten siete cartas: dos propias para cada jugador y cinco comunitarias. La mano final se forma con las mejores cinco cartas posibles.

¿Cuántas rondas de apuestas hay en una partida?
Hay tres rondas. Puedes apostar tras recibir tus dos cartas, después del flop o al final, una vez vistas todas las cartas. Cuanto antes apuestes, mayor puede ser tu apuesta.

¿Qué pagos se pueden conseguir con la apuesta Trips?
La apuesta paralela Trips premia si consigues un trío o mejor. Los pagos van de 3 a 1 por un trío hasta 50 a 1 por una escalera real, según la tabla.

¿Qué ocurre si el crupier no tiene una mano válida para abrir?
Si el crupier no tiene al menos una pareja, no abre. En ese caso, la apuesta inicial se devuelve y la ciega se paga según la tabla de premios.

¿Sirven los trucos del Blackjack para este juego?
No. Aunque puede haber estrategias básicas, los trucos del Blackjack no se aplican aquí. Ultimate Texas Hold’em tiene sus propias reglas.

¿Tienen algo en común el póker y el blackjack?

Sí, el blackjack y el póker comparten varias cosas: ambos se juegan con baraja francesa, en mesa, contra el crupier (en el caso del poker, depende de la variante), y los dos combinan azar con estrategia. 

 

Aviso: Todos los consejos dados en este artículo tienen un carácter meramente informativo basado en bibliografía sobre juegos de azar. Sin embargo ninguno de estos consejos garantiza ni es un elemento determinante para el éxito en la actividad del juego analizado. En nuestro blog tratamos temáticas relacionadas con el mundo de los juegos y los contenidos son informativos y no significa que tengamos disponible el juego, producto, utensilio, accesorio, etcétera…del que habla el artículo.

• Las mejores apuestas son las más sencillas: línea de pase y apuesta de probabilidades. 
• Huye de las apuestas con nombres llamativos. Los dados no tienen memoria: que un número haya salido cinco veces no significa que vaya a repetirse.
• Conoce las reglas, respeta a los demás jugadores y nunca digas "siete" en voz alta.

Los dados (craps) son uno de los juegos más populares del casino y también uno de los peor entendidos. Si alguna vez has pasado por delante de una mesa de dados, habrás notado que hay gritos, fichas volando y un tapete lleno de casillas que parecen un jeroglífico. Normal que muchos jugadores se sienten a la mesa y apuesten por instinto sin tener muy claro lo que están haciendo.
Es un error más común de lo que parece, y no solo en los dados. Pasa en el blackjack, donde casi nadie sigue la estrategia básica. Y pasa en la ruleta, donde muchos eligen la ruleta americana sin saber que el casino gana el doble que en la europea.
En los dados la confusión es todavía mayor, porque hay decenas de apuestas posibles y la mayoría están diseñadas para que gane la casa. Por eso hemos preparado esta guía con los 7 errores más comunes y cómo evitarlos.

1. Jugar a apuestas matemáticamente poco ganadoras

Cuando miras el tapete de una mesa de dados o craps, verás varios números marcados: 4, 5, 6, 8, 9 y 10. Puedes apostar a que cualquiera de ellos saldrá antes que el 7. Eso es una apuesta de lugar (Place). Muchos jugadores novatos apuestan a todos o casi todos esos números a la vez, creyendo que así es más fácil ganar. El problema es que cada una de esas apuestas lleva su propia comisión oculta a favor del casino.
¿Cuánto se lleva el casino en cada una? Depende del número. Si apuestas al 4 o al 10, el casino tiene un 6,67% de ventaja, es decir, de cada 100 que apuestes, espera quedarse con casi 7. Si apuestas al 5 o al 9, la ventaja baja al 4%. Y si apuestas al 6 o al 8, el casino solo tiene un 1,52% de ventaja, que es la opción menos mala.
La conclusión es clara: si vas a hacer apuestas de lugar, limítate al 6 y al 8. Todo lo demás es regalar dinero al casino.

2. Abusar de las apuestas de lugar o de apuestas llamativas

Además de las apuestas de lugar, en la mesa de dados existen apuestas a números sueltos como el 2, 3, 11 o el 12. Suenan tentadoras porque pagan mucho si salen, pero salen muy poco. El casino lo sabe y por eso se queda con un margen enorme: entre el 5,56% y hasta un 20-25% de todo lo que apuestes.
En algunos casinos, especialmente en Las Vegas, también encontrarás apuestas con nombres llamativos como la Fire Bet o la High-Low. No te dejes engañar: cuanto más vistoso es el nombre, más gana el casino con esa apuesta.
Una forma fácil de protegerte: si ves una apuesta en la mesa que no reconoces o que no entiendes bien cómo funciona, no pongas dinero en ella. Casi seguro que está diseñada para que el casino gane más.

3. Confiar en las tendencias

Si el 6 ha salido tres veces seguidas, muchos jugadores piensan que va a seguir saliendo y apuestan fuerte a ese número. Otros piensan justo lo contrario: que ya 'toca' que salga otro. Ambos se equivocan.
Los dados no tienen memoria. Cada tirada es completamente independiente de la anterior, y que un número haya salido cinco veces seguidas no hace ni más ni menos probable que vuelva a salir. Esto es lo que los expertos llaman la 'falacia del jugador', y es una de las trampas mentales más comunes en cualquier juego de azar.
Pasa exactamente igual en la ruleta: no hay ningún sistema que permita predecir qué número saldrá a continuación. Si alguien te dice que tiene un método infalible basado en rachas o tendencias, desconfía.

4. Ignorar la apuesta de probabilidades 

De todas las apuestas que puedes hacer en una mesa de dados, la mayoría están diseñadas para que el casino gane más. Pero hay cuatro que son mucho más favorables para el jugador: la línea de pase, la apuesta de venir, y sus contrarias (no pasa y no venir). En estas cuatro, el casino solo se queda con un 1,4% de lo que apuestas, que es una de las ventajas más bajas que encontrarás en cualquier juego de casino.
Y aquí viene el truco que pocos jugadores conocen: después de hacer una de esas cuatro apuestas, puedes añadir una apuesta extra llamada apuesta de probabilidades. ¿Qué tiene de especial? Que el casino no se lleva absolutamente nada. Cero. Es el único caso en todo el casino donde juegas en igualdad de condiciones con la casa.
Entonces, ¿cuál es la jugada inteligente? Apostar lo mínimo en la línea de pase (porque ahí el casino sí se lleva su parte) y poner el máximo en la apuesta de probabilidades (donde no se lleva nada). Es así de sencillo.

5. No estudiar las probabilidades antes de sentarse a la mesa

Imagina que entras en una mesa de dados y ves una apuesta que el casino anuncia como 'especial' o 'para jugadores expertos'. Suena bien, ¿verdad? Pues casi siempre significa lo contrario: cuanto más la promociona el casino, más dinero gana con ella.
El verdadero jugador inteligente es el que conoce los números antes de sentarse. Un error muy común es repartir el dinero a partes iguales entre la línea de pase y la apuesta de probabilidades. Como hemos visto, en la línea de pase el casino se lleva su parte, pero en la apuesta de probabilidades no se lleva nada. La estrategia lógica es poner lo mínimo en la línea de pase y destinar el máximo a la apuesta de probabilidades.
Si todo esto te suena a chino, no te preocupes: es normal. Los dados tienen su propio vocabulario (tirador, punto, tirada de salida...) y al principio puede resultar confuso. Pero dedicar media hora a aprender los términos básicos antes de jugar a los dados te ahorrará mucho dinero y muchos dolores de cabeza.

6. Descuidar la técnica de lanzamiento

Nadie puede controlar qué número va a salir en los dados. Pero eso no significa que la forma de lanzarlos dé igual. Un buen lanzamiento no te hará ganar, pero uno malo puede arruinarte la tirada y ganarte algún que otro reproche del crupier.
Lo básico: no aprietes los dados, lánzalos con suavidad y procura que golpeen la pared del fondo de la mesa, porque si no lo hacen, el crupier puede anular la tirada. Lanza desde una altura cómoda, sin levantar demasiado el brazo, con un movimiento fluido.
¿Se puede aprender a lanzar mejor? Sí, pero con matices. Algunos jugadores veteranos entrenan durante años lo que llaman 'control del lanzamiento'. La idea no es elegir qué número sale (eso es imposible), sino conseguir que el temido 7 aparezca un poco menos de lo habitual. ¿Funciona? No hay pruebas científicas, pero tampoco hace daño practicar.

7. No respetar el protocolo de la mesa

La mesa de dados es como cualquier juego con amigos: tiene sus normas no escritas, y si las rompes, todo el mundo se incomoda. No hace falta memorizar un manual de protocolo, pero hay cosas que nunca debes hacer.
Cuando alguien está a punto de lanzar, aparta las manos de la mesa. No tires fichas mientras los dados están en el aire. Y si estás perdiendo, guárdatelo para ti: nadie quiere oír lamentos ajenos mientras juega.
Si el lanzador lleva una buena racha, puedes celebrar, pero sin agobiarle. Dale su espacio y no te acerques demasiado durante el lanzamiento.
Y la regla de oro: jamás digas 'siete' en voz alta. El 7 hace perder a casi toda la mesa, así que pronunciarlo es como gafar a todos los jugadores de golpe. Es superstición, sí, pero hazlo y no serás bienvenido en ese casino.

Estrategias básicas para jugadores principiantes

Si acabas de llegar al mundo de los dados, la mejor estrategia es también la más simple: apuesta a la línea de pase y añade el máximo posible en la apuesta de probabilidades. Con eso ya estás jugando con una de las ventajas más bajas de todo el casino.
Cuando tengas más experiencia, puedes explorar las apuestas de no pasa y no venir, que consisten en apostar en contra del lanzador. Esto te permite cubrir varios resultados a la vez y reducir pérdidas. Pero lo más importante, seas principiante o veterano, es la disciplina: decide cuánto estás dispuesto a perder antes de sentarte, no intentes recuperar lo perdido subiendo las apuestas, y levántate cuando toque.
¿Y si nunca has pisado una mesa de dados? Practica gratis online. Hay simuladores que te permiten probar todas las apuestas sin arriesgar un céntimo, y son la mejor forma de llegar preparado a una mesa de verdad.

Aviso: Todos los consejos dados en este artículo tienen un carácter meramente informativo basado en bibliografía sobre juegos de azar. Sin embargo ninguno de estos consejos garantiza ni es un elemento determinante para el éxito en la actividad del juego analizado. En nuestro blog tratamos temáticas relacionadas con el mundo de los juegos y los contenidos son informativos y no significa que tengamos disponible el juego, producto, utensilio, accesorio, etcétera…del que habla el artículo.